题目内容
有两个函数f(x)=asin(kx+ ),g(x)=btan(kx-
),g(x)=btan(kx- )(k>0),它们的周期之和为
)(k>0),它们的周期之和为 且f(
且f( )=g(
)=g( ),
),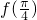 =-
=- 求这两个函数,并求g(x)的单调递增区间.
求这两个函数,并求g(x)的单调递增区间.
解:由条件得 ,∴k=2.
,∴k=2.
由f( )=g(
)=g( ),得a=2b①
),得a=2b①
由f( )=-
)=- g(
g( )+1,得a=2-2b②
)+1,得a=2-2b②
∴由①②解得a=1,b= .
.
∴f(x)=sin(2x+ ),g(x)=
),g(x)= tan(2x-
tan(2x- ).
).
∴当- +kπ<2x-
+kπ<2x- <
< +kπ,k∈Z时,g(x)单调递增.
+kπ,k∈Z时,g(x)单调递增.
∴g(x)的单调递增区间为: k∈Z.
k∈Z.
分析:由题义及函数解析式求出其函数周期,在利用已知等式条件建立a,b的方程,求解即可找出其函数单调区间.
点评:此题考查了三角函数的周期求法,及利用方程解未知量的方程思想,还考查了三角函数单调性.
 ,∴k=2.
,∴k=2.由f(
 )=g(
)=g( ),得a=2b①
),得a=2b①由f(
 )=-
)=- g(
g( )+1,得a=2-2b②
)+1,得a=2-2b②∴由①②解得a=1,b=
 .
.∴f(x)=sin(2x+
 ),g(x)=
),g(x)= tan(2x-
tan(2x- ).
).∴当-
 +kπ<2x-
+kπ<2x- <
< +kπ,k∈Z时,g(x)单调递增.
+kπ,k∈Z时,g(x)单调递增.∴g(x)的单调递增区间为:
 k∈Z.
k∈Z.分析:由题义及函数解析式求出其函数周期,在利用已知等式条件建立a,b的方程,求解即可找出其函数单调区间.
点评:此题考查了三角函数的周期求法,及利用方程解未知量的方程思想,还考查了三角函数单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目