题目内容
.如图2-13,已知⊙O外一点P,作⊙O的切线PQ,Q为切点,过PQ中点M,作割线MAB,交⊙O于点A、B,连结PA并延长交⊙O于C,连结PB交⊙O于点D,求证:CD∥PQ.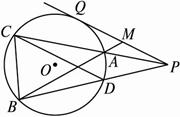
图2-13
思路分析:本题要证CD∥PQ,只要证∠ACD =∠APQ,又∠ACD=∠ABD,因而只需证∠ABD =∠APQ,这可利用相似三角形证得.
证明:∵PQ切⊙O于Q,?
∴MQ2=MA·MB.?
又∵M为PQ中点,即MQ =MP,?
∴MP2=MA·MB,即![]() =
=![]() .?
.?
又∠AMP =∠PMB,?
∴△AMP∽△PMB.∴∠MPA =∠ABD.?
又∵∠ABD =∠ACD,?
∴∠MPA =∠ACD.∴CD∥PQ.

练习册系列答案
相关题目
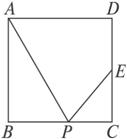
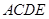 所在的平面
所在的平面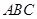 ,
,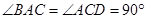 ,
,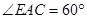 ,
,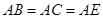 . (1)在直线
. (1)在直线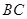 上是否存在一点
上是否存在一点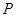 ,使得
,使得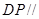 平面
平面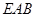 ?请证明你的结论;
?请证明你的结论;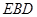 与平面
与平面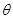 的余弦值。
的余弦值。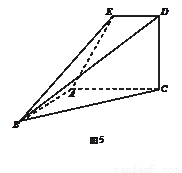
 (2)若
(2)若