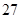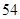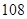题目内容
)已知数列{an}是首项为-1,公差d 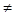 0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
(1)求{an}的通项公式;
(2)若Cn=an·bn,求数列{Cn}的前n项和Sn。
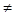 0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。(1)求{an}的通项公式;
(2)若Cn=an·bn,求数列{Cn}的前n项和Sn。
(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)由首项
 及
及 可求出公差
可求出公差 ,从而得通项公式
,从而得通项公式 ;(2)易得
;(2)易得 ,所以
,所以 .凡是等差数列与等比数列的积构成的数列,都用错位相消法求和.
.凡是等差数列与等比数列的积构成的数列,都用错位相消法求和. 试题解析:(1)由题意知:
 ,
,即
 , 2分
, 2分 得
得 4分
4分
 6分
6分(2)由题意
 ,所以
,所以 ,
,
 8分
8分




 12分
12分
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
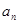 }的首项a1=1,公差d>0,且
}的首项a1=1,公差d>0,且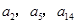 分别是等比数列{
分别是等比数列{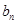 }的b2,b3,b4.
}的b2,b3,b4.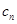 }对任意自然数n均有
}对任意自然数n均有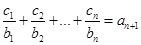 成立,求
成立,求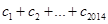 的值.
的值.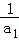 +
+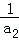 +…+
+…+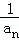 <
<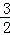 .
. 中,已知
中,已知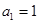 ,
,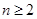 时,
时,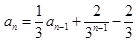 .数列
.数列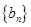 满足:
满足: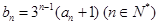 .
.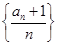 的前
的前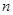 项和为
项和为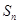 ,若不等式
,若不等式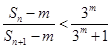 成立(
成立(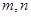 为正整数).求出所有符合条件的有序实数对
为正整数).求出所有符合条件的有序实数对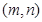 .
. 中,
中,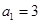 ,
,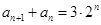 ,
,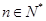 .
.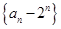 是等比数列,并求数列
是等比数列,并求数列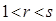 且
且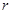 ,
,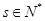 ,求证:使得
,求证:使得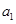 ,
,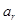 ,
,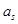 成等差数列的点列
成等差数列的点列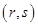 在某一直线上.
在某一直线上.
 ,
, ”时,从“
”时,从“ ”到“
”到“ ”左边需要添加的代数式为( )
”左边需要添加的代数式为( )



 行的第2个数为 .
行的第2个数为 .
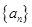 为等差数列,若
为等差数列,若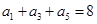 ,
,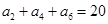 ,则公差
,则公差 .
.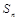 为等差数列
为等差数列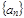 的前
的前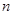 项和,
项和,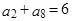 ,则
,则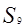 为( )
为( )