题目内容
给出如下三个函数:①f(x)=(x-1)3;②f(x)=k(x-1) (k<0);③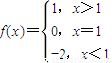
则同时满足性质:(1)对于任意的x1,x2∈R(x1≠x2),有
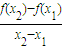 >0;(2)图象关于点(1,0)成中心对称图形的函数序号为 .
>0;(2)图象关于点(1,0)成中心对称图形的函数序号为 .
【答案】分析:性质(1)对于任意的x1,x2∈R(x1≠x2),有 >0表示,函数在R上为增函数,性质(2)图象关于点(1,0)成中心对称图形表示函数f(x+1)为奇函数,则①即满足(1)也满足(2),②不满足(1),③不满足(1),易得到答案.
>0表示,函数在R上为增函数,性质(2)图象关于点(1,0)成中心对称图形表示函数f(x+1)为奇函数,则①即满足(1)也满足(2),②不满足(1),③不满足(1),易得到答案.
解答:解:f(x)=(x-1)3可以看成
f(x)=x3向右平移一个单位得到的函数.
又 >0,则f(x)为增函数.
>0,则f(x)为增函数.
故只有①满足.
故答案为:①
点评:函数的性质有不同的表达方式,我们要注意定义之外的其它表达方式,如本题中,“对于任意的x1,x2∈R(x1≠x2),有 >0表示,函数在R上为增函数”等.
>0表示,函数在R上为增函数”等.
 >0表示,函数在R上为增函数,性质(2)图象关于点(1,0)成中心对称图形表示函数f(x+1)为奇函数,则①即满足(1)也满足(2),②不满足(1),③不满足(1),易得到答案.
>0表示,函数在R上为增函数,性质(2)图象关于点(1,0)成中心对称图形表示函数f(x+1)为奇函数,则①即满足(1)也满足(2),②不满足(1),③不满足(1),易得到答案.解答:解:f(x)=(x-1)3可以看成
f(x)=x3向右平移一个单位得到的函数.
又
 >0,则f(x)为增函数.
>0,则f(x)为增函数.故只有①满足.
故答案为:①
点评:函数的性质有不同的表达方式,我们要注意定义之外的其它表达方式,如本题中,“对于任意的x1,x2∈R(x1≠x2),有
 >0表示,函数在R上为增函数”等.
>0表示,函数在R上为增函数”等. 
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
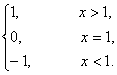 则不同时满足性质:
则不同时满足性质: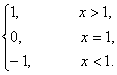 则不同时满足性质:
则不同时满足性质: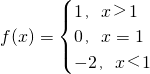
 >0;(2)图象关于点(1,0)成中心对称图形的函数序号为______.
>0;(2)图象关于点(1,0)成中心对称图形的函数序号为______.