题目内容
如图,已知直线l1:2x-y-4=0,l2:y=kx+b.为了使l1到l2的角为45°,且交点在第一象限,试确定k和b的值.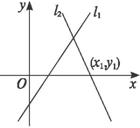
思路解析：可由到角公式求出k值;又交点在第一象限,可以限定b的范围.
解：由tan45°=
,即
=1,
解得k=-3.∴l2:y=-3x+b.
由
解得y=
.∵
＞0,∴b＞6.
∴k=-3,b＞6即为所求.
误区警示
一定要注意l1到l2的角为45°,与l2到l1的角为45°是不同的.
练习册系列答案
阅读快车系列答案
相关题目
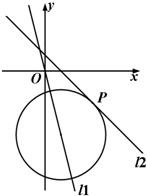如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．
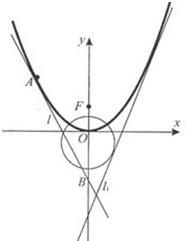如图，已知直线l1：y=2x+m（m＜0）与抛物线C1：y=ax2（a＞0）和圆C2：x2+（y+1）2=5都相切，F是C1的焦点．
如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．求有圆心在l1上且与直线l2相切于点P的圆的方程．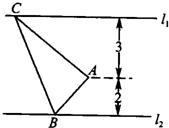
如图，已知直线l1∥l2，点A是l1，l2之间的定点，点A到l1，l2之间的距离分别为3和2，点B是l2上的一动点，作AC⊥AB，且AC与l1交于点C，则△ABC的面积的最小值为
如图，已知直线l1∥l2，点A是l1，l2上两直线之间的动点，且到l1距离为4，到l2距离为3，若