题目内容
如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN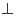 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证:
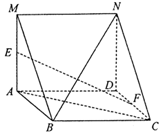 (1)EF//平面MNCB;
(1)EF//平面MNCB;
(2)平面MAC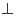 平面BND.
平面BND.
证明:(1)取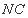 的中点
的中点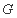 ,连接
,连接 ,
,
因为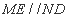 且
且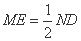 ,
,
又因为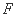 、
、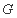 分别为
分别为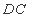 、
、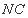 的中点,
的中点,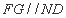 且
且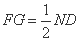 ,
,
所以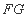 与
与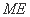 平行且相等,所以四边形
平行且相等,所以四边形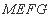 是平行四边形,所以
是平行四边形,所以 ,
,
又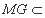 平面
平面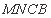 ,
,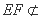 平面
平面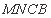 ,所以
,所以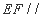 平面
平面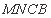
(2)连接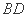 、
、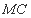 ,因为四边形
,因为四边形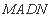 是矩形,所以
是矩形,所以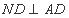 ,又因为平面
,又因为平面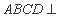 平面
平面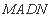 ,所以
,所以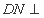 平面
平面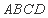 ,所以
,所以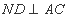
因为四边形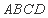 是菱形,所以
是菱形,所以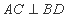 ,因为
,因为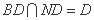 ,所以
,所以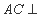 平面
平面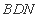
又因为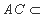 平面
平面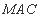 ,所以
,所以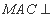 平面
平面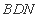

练习册系列答案
相关题目
 在
在 (0,+
(0,+ )上为减函数,则
)上为减函数,则 的值为 .
的值为 . 的偶函数
的偶函数 满足对任意的
满足对任意的 ,都有
,都有 ,且当
,且当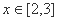 时,
时,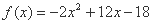 ,若函数
,若函数 在
在 上至少有 三个零点,则
上至少有 三个零点,则 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
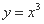 与
与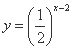 的图象的交点为
的图象的交点为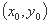 ,则
,则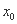 所在的区间是 ( )
所在的区间是 ( )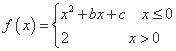 ,若
,若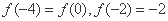 ,则关于
,则关于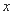 的方程
的方程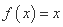 的解的个数为_____个
的解的个数为_____个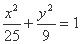 的右焦点且倾斜角为45°的弦AB的长为( )
的右焦点且倾斜角为45°的弦AB的长为( )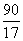 D.7
D.7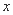 轴,且过点
轴,且过点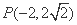 ,则抛物线的方程为
,则抛物线的方程为  的直线都可以用方程
的直线都可以用方程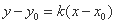 表示
表示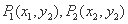 的直线都可以用方程
的直线都可以用方程 表示
表示 表示
表示 的直线都可以用方程
的直线都可以用方程 表示
表示