题目内容
17.函数f(x)=log3(4x-1)的定义域为( )| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2},+∞$) | C. | ($\frac{1}{4},\frac{1}{2}$] | D. | ($\frac{1}{4},+∞$) |
分析 由对数有意义可得4x-1>0,解不等式可得函数的定义域.
解答 解:由对数有意义可得4x-1>0,
解不等式可得x>$\frac{1}{4}$,
∴函数的定义域为($\frac{1}{4}$,+∞)
故选:D
点评 本题考查对数函数的定义域,属基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
7.在椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1中,过点P(1,1)的弦被点P平分,则此弦所在的直线方程为( )
| A. | x+2y-3=0 | B. | x-2y-3=0 | C. | x+2y+3=0 | D. | x-2y+3=0 |
8.在区间(-∞,0)上单调递增的函数是( )
| A. | y=2x | B. | y=log2x | C. | y=$\frac{2}{x}$ | D. | y=-2x |
9.已知R为实数集,M=$\left\{{y\left|{y=\sqrt{1+x}}\right.}\right\}$,$N=\left\{{x|y=\sqrt{x-1}}\right\}$,则M∩(∁RN)=( )
| A. | {x|0≤x<1} | B. | {x|-1≤x<1} | C. | {x|-1≤x≤0} | D. | {x|0≤x≤1} |
7.在△ABC中,角A、B、C所对的边分别是a、b、c,满足acosA+bcosB=ccosC,则△ABC为( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 直角三角形 |
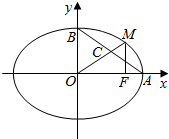 如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.
如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.