题目内容
已知函数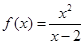 (x∈R,且x≠2).
(x∈R,且x≠2).
(1)求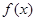 的单调区间;
的单调区间;
(2)若函数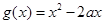 与函数
与函数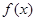 在x∈[0,1]上有相同的值域,求a的值.
在x∈[0,1]上有相同的值域,求a的值.
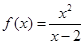 (x∈R,且x≠2).
(x∈R,且x≠2).(1)求
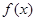 的单调区间;
的单调区间;(2)若函数
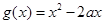 与函数
与函数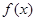 在x∈[0,1]上有相同的值域,求a的值.
在x∈[0,1]上有相同的值域,求a的值.(1)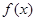 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 ;(2)
;(2) .
.
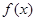 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 ;(2)
;(2) .
.试题分析:解题思路(1)分离参数转化从基本不等式求最值;(2)由(1)得出
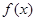 的值域,再利用一元二次函数的单调性求
的值域,再利用一元二次函数的单调性求 值.规律总结:涉及分式求最值,往往利用分离参数法,出现定值,以便运用基本不等式求解;求一元二次函数的值域要注意运用数形结合思想.
值.规律总结:涉及分式求最值,往往利用分离参数法,出现定值,以便运用基本不等式求解;求一元二次函数的值域要注意运用数形结合思想.试题解析:(1)
 ,
,令
 ,由于
,由于 在
在 内单调递增,在
内单调递增,在 内单调递减,∴容易求得
内单调递减,∴容易求得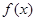 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 .
.(2)∵
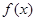 在
在 上单调递减,∴其值域为
上单调递减,∴其值域为 ,
,即
 时,
时, .
.∵
 为最大值,∴最小值只能为
为最大值,∴最小值只能为 ,
,若
 ,则
,则 ;若
;若 ,则
,则 ;
;综上得
 .
.
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 ,
,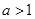 .
. 的单调性;
的单调性; 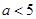 ,则对任意
,则对任意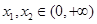 ,
,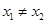 ,有
,有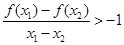 .
. (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式 ,
, 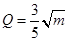 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资 (单位:万元)
(单位:万元) (单位:万元)关于
(单位:万元)关于 .
.
 表示
表示 的面积;
的面积; (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为 (
( ).
). 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内?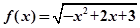 的定义域为 ;
的定义域为 ;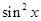 -sin x+2的最大值是 ( ).
-sin x+2的最大值是 ( ).
 ,则
,则 .
.