题目内容
函数f(x)=(sinx+3)(cosx-3)的值域为________.

分析:利用t=sinx+cosx,利用两角和的正弦公式进行化简后,由x的范围求出t的范围,由对t的式子两边平方后,由平方关系求出sinxcosx,代入解析式转化为关于t的二次函数,对式子配方后利用二次函数的性质求出最值,就求出值域;
解答:f(x)=(sinx+3)(cosx-3)=sinxcosx-3sinx+3cosx-9
令cosx-sinx=t,则(cosx-sinx)2=cos2x-2sinxcosx+sin2x=1-2sinxcosx=t2
∴sinxcosx=
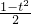
整理得f(x)=
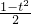 +3t-9=-
+3t-9=-
∵t=cosx-sinx=-
 sin(x+θ)
sin(x+θ)由-1≤sin(x+θ)≤1可知-
 ≤t≤
≤t≤ ,
,将t的取值代入f(x)中可知

∴f(x)的值域为
 ,
,故答案为:

点评:本题的考点是复合三角函数的值域的求法,主要利用换元法和“sinx+cosx”与“sinxcosx”的关系,注意由函数的定义域和正弦(余弦)函数的值域,求出换元后的自变量的范围,根据二次函数的性质求出函数的值域.

练习册系列答案
相关题目
函数f(x)=
ex(sinx+cosx)在区间[0,
]上的值域为( )
| 1 |
| 2 |
| π |
| 2 |
A、[
| ||||||
B、(
| ||||||
C、[1,e
| ||||||
D、(1,e
|
 已知函数f(x)=2cosx(sinx-cosx)+1.
已知函数f(x)=2cosx(sinx-cosx)+1.