题目内容
已知椭圆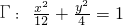 .
.
(1)直线AB过椭圆Γ的中心交椭圆于A、B两点,C是它的右顶点,当直线AB的斜率为1时,求△ABC的面积;
(2)设直线l:y=kx+2与椭圆Γ交于P、Q两点,且线段PQ的垂直平分线过椭圆Γ与y轴负半轴的交点D,求实数k的值.
解:(1)依题意,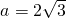 ,
,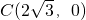 ,直线AB的方程为y=x,
,直线AB的方程为y=x,
由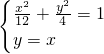 ,得
,得 ,
,
设A(x1,y1)B(x2,y2),∵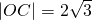 ,
,
∴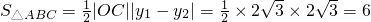 ;
;
(2)由 得(3k2+1)x2+12kx=0,△=(12k)2≥0,
得(3k2+1)x2+12kx=0,△=(12k)2≥0,
依题意,k≠0,设P(x1,y1),Q(x2,y2),线段PQ的中点H(x0,y0),
则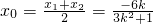 ,
,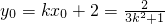 ,D(0,-2),
,D(0,-2),
由kDH•kPQ=-1,得 ,解得
,解得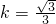 .
.
所以实数k的值为 .
.
分析:(1)由题意写出C点坐标,直线AB方程,联立直线方程与椭圆方程可求得交点A、B的纵坐标,设A(x1,y1),B(x2,y2),则 ,代入数值即可求得面积;
,代入数值即可求得面积;
(2)联立直线l与椭圆方程消掉y得x的二次方程,设P(x1,y1),Q(x2,y2),线段PQ的中点H(x0,y0),由韦达定理及中点坐标公式可用k表示出中点坐标,由垂直可得
kDH•kPQ=-1,解出即得k值,注意检验△>0;
点评:本题考查直线与圆锥曲线的位置关系、三角形面积公式,韦达定理、判别式是解决该类题目的常用知识,要熟练掌握.
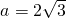 ,
,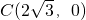 ,直线AB的方程为y=x,
,直线AB的方程为y=x,由
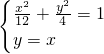 ,得
,得 ,
,设A(x1,y1)B(x2,y2),∵
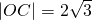 ,
,∴
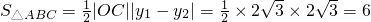 ;
;(2)由
 得(3k2+1)x2+12kx=0,△=(12k)2≥0,
得(3k2+1)x2+12kx=0,△=(12k)2≥0,依题意,k≠0,设P(x1,y1),Q(x2,y2),线段PQ的中点H(x0,y0),
则
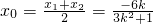 ,
,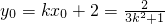 ,D(0,-2),
,D(0,-2),由kDH•kPQ=-1,得
 ,解得
,解得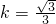 .
.所以实数k的值为
 .
.分析:(1)由题意写出C点坐标,直线AB方程,联立直线方程与椭圆方程可求得交点A、B的纵坐标,设A(x1,y1),B(x2,y2),则
 ,代入数值即可求得面积;
,代入数值即可求得面积;(2)联立直线l与椭圆方程消掉y得x的二次方程,设P(x1,y1),Q(x2,y2),线段PQ的中点H(x0,y0),由韦达定理及中点坐标公式可用k表示出中点坐标,由垂直可得
kDH•kPQ=-1,解出即得k值,注意检验△>0;
点评:本题考查直线与圆锥曲线的位置关系、三角形面积公式,韦达定理、判别式是解决该类题目的常用知识,要熟练掌握.

练习册系列答案
相关题目