题目内容
已知椭圆
+y2=1,直线x+y-4=0,及椭圆左准线l,椭圆上点P到x+y-4=0的距离为m,到l的距离为n,则m+
n的最小值为( )
| x2 |
| 2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
| C、5 | ||||
D、5
|
分析:设出P的坐标为(
cosα,sinα),根据椭圆方程找出椭圆的左准线方程,然后利用点到直线的距离公式表示出P到x+y-4=0的距离m,表示出P到准线l的距离n,把表示出的m与n代入m+
n中,然后利用三角函数的方法求出最小值即可.
| 2 |
| ||
| 2 |
解答:解:设P(
cosα,sinα),由椭圆的方程得到左准线l的方程为x=-2,
由题意得:m=
,n=|
cosα+2|,
则m+
n=
+
≥
=
(其中sinβ=
,cosβ=
)
当sin(β+α)=-1时,m+
n≥
=
,
所以m+
n的最小值为
.
故选A
| 2 |
由题意得:m=
|
| ||
|
| 2 |
则m+
| ||
| 2 |
|
| ||
|
|
| ||
|
|2
| ||
|
| |3sin(β+α)-2| | ||
|
2
| ||
| 3 |
| 1 |
| 3 |
当sin(β+α)=-1时,m+
| ||
| 2 |
| 5 | ||
|
5
| ||
| 2 |
所以m+
| ||
| 2 |
5
| ||
| 2 |
故选A
点评:此题考查学生掌握椭圆的简单性质,灵活运用点到直线的距离公式化简求值,是一道综合题.

练习册系列答案
相关题目
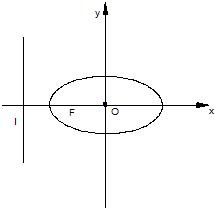 已知椭圆
已知椭圆 已知椭圆
已知椭圆