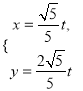Question

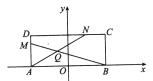
【题目】【2018衡水金卷（二）】如图，矩形中， 且， 交于点．

（I）若点的轨迹是曲线的一部分，曲线关于轴、轴、原点都对称，求曲线的轨迹方程；

（II）过点作曲线的两条互相垂直的弦，四边形的面积为，探究是否为定值？若是，求出此定值，若不是，请说明理由．

Answer 1

【答案】（I）曲线的轨迹方程为；（II）为定值．

【解析】试题分析：（1）可得M（﹣2，2λ），N（﹣2+4λ，2），，设Q（x，y），整理得： ，即可得曲线P的轨迹方程为；

（2）设直线的斜率为，把代入椭圆方程，化简整理得.利用韦达定理易得四边形GFHE的面积为， ，所以，

试题解析：

(1)设，

由,

求得,

∵,

∴,

∴，

整理得.

可知点的轨迹为第二象限的椭圆，由对称性可知曲线的轨迹方程为.

（2）设，当直线斜率存在且不为零时，设直线的斜率为，把代入椭圆方程，化简整理得.

，

.

∴

.

∵,

∴把换成，即得.

∴

，

，

，

∴.

当直线斜率不存在或为零时，

.

∴为定值.