题目内容
已知函数 为常数),数列{an}满足:
为常数),数列{an}满足: ,an+1=f(an),n∈N*.
,an+1=f(an),n∈N*.
(1)当α=1时,求数列{an}的通项公式;
(2)在(1)的条件下,证明对?n∈N*有: ;
;
(3)若α=2,且对?n∈N*,有0<an<1,证明: .
.
解:(1)当α=1时, ,两边取倒数,得
,两边取倒数,得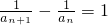 ,----(2分)
,----(2分)
故数列 是以
是以 为首项,1为公差的等差数列,
为首项,1为公差的等差数列, ,
,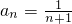 ,n∈N*.--------------(4分)
,n∈N*.--------------(4分)
(2)证法1:由(1)知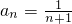 ,故对k=1,2,3…
,故对k=1,2,3… =
= -------------(6分)
-------------(6分)
∴a1a2a3+a2a3a4+…+anan+1an+2
=
= =
= .------------------------------(9分).
.------------------------------(9分).
[证法2:①当n=1时,等式左边= ,
,
等式右边= ,左边=右边,等式成立;-------------------------(5分)
,左边=右边,等式成立;-------------------------(5分)
②假设当n=k(k≥1)时等式成立,
即 ,
,
则当n=k+1时
=
=
这就是说当n=k+1时,等式成立,----------------------------------------(8分)
综①②知对于?n∈N*有: .----(9分)]
.----(9分)]
(3)当α=2时, 则
则 ,-------------------(10分)
,-------------------(10分)
∵0<an<1,
∴ --------------------------------(11分)=
--------------------------------(11分)= =
=
 =
= .--------------------(13分)
.--------------------(13分)
∵an=1-an与 不能同时成立,∴上式“=”不成立,
不能同时成立,∴上式“=”不成立,
即对?n∈N*, .-----------------------------------------------------------(14分)
.-----------------------------------------------------------(14分)
证法二:当α=2时, ,
,
则 ----------------------------------------------------(10分)
----------------------------------------------------(10分)
又0<an<1,∴ ,
,
∴an+1>an,∴an∈[ ,1),n∈N*------------------------------------------------(11分)
,1),n∈N*------------------------------------------------(11分)
令 ,则
,则 ,--------------------------(12分)
,--------------------------(12分)
当 ,所以函数g(x)在
,所以函数g(x)在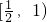 单调递减,故当
单调递减,故当 ,所以命题得证------------------(14分)
,所以命题得证------------------(14分)
所以命题得证-----------------------------------------(14分)
分析:(1)当α=1时,说明数列 是以
是以 为首项,1为公差的等差数列,然后求数列{an}的通项公式;
为首项,1为公差的等差数列,然后求数列{an}的通项公式;
(2)法一:在(1)的条件下,化简数列的通项公式,利用裂项法:证明对?n∈N*有: ;
;
法二:直接利用数学归纳法的证明步骤证明即可.
(3)法一:通过α=2,化简an+1-an的表达式为 ,利用基本不等式直接证明
,利用基本不等式直接证明 .
.
法二:通过 ,以及0<an<1,说明
,以及0<an<1,说明 ,an∈[
,an∈[ ,1),n∈N*,构造函数
,1),n∈N*,构造函数 ,利用函数的导数,求出函数的最大值即可证明结果.
,利用函数的导数,求出函数的最大值即可证明结果.
点评:本题考查数列与函数的综合应用,数学归纳法的证明方法,构造法以及函数的导数求解函数的最大值证明不等式,基本不等式的应用,考查分析问题解决问题的能力,转化思想的应用.
 ,两边取倒数,得
,两边取倒数,得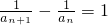 ,----(2分)
,----(2分)故数列
 是以
是以 为首项,1为公差的等差数列,
为首项,1为公差的等差数列, ,
,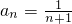 ,n∈N*.--------------(4分)
,n∈N*.--------------(4分)(2)证法1:由(1)知
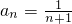 ,故对k=1,2,3…
,故对k=1,2,3… =
= -------------(6分)
-------------(6分)∴a1a2a3+a2a3a4+…+anan+1an+2
=

=
 =
= .------------------------------(9分).
.------------------------------(9分).[证法2:①当n=1时,等式左边=
 ,
,等式右边=
 ,左边=右边,等式成立;-------------------------(5分)
,左边=右边,等式成立;-------------------------(5分)②假设当n=k(k≥1)时等式成立,
即
 ,
,则当n=k+1时

=

=

这就是说当n=k+1时,等式成立,----------------------------------------(8分)
综①②知对于?n∈N*有:
 .----(9分)]
.----(9分)](3)当α=2时,
 则
则 ,-------------------(10分)
,-------------------(10分)∵0<an<1,
∴
 --------------------------------(11分)=
--------------------------------(11分)= =
=
 =
= .--------------------(13分)
.--------------------(13分)∵an=1-an与
 不能同时成立,∴上式“=”不成立,
不能同时成立,∴上式“=”不成立,即对?n∈N*,
 .-----------------------------------------------------------(14分)
.-----------------------------------------------------------(14分)证法二:当α=2时,
 ,
,则
 ----------------------------------------------------(10分)
----------------------------------------------------(10分)又0<an<1,∴
 ,
,∴an+1>an,∴an∈[
 ,1),n∈N*------------------------------------------------(11分)
,1),n∈N*------------------------------------------------(11分)令
 ,则
,则 ,--------------------------(12分)
,--------------------------(12分)当
 ,所以函数g(x)在
,所以函数g(x)在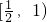 单调递减,故当
单调递减,故当 ,所以命题得证------------------(14分)
,所以命题得证------------------(14分)所以命题得证-----------------------------------------(14分)
分析:(1)当α=1时,说明数列
 是以
是以 为首项,1为公差的等差数列,然后求数列{an}的通项公式;
为首项,1为公差的等差数列,然后求数列{an}的通项公式;(2)法一:在(1)的条件下,化简数列的通项公式,利用裂项法:证明对?n∈N*有:
 ;
;法二:直接利用数学归纳法的证明步骤证明即可.
(3)法一:通过α=2,化简an+1-an的表达式为
 ,利用基本不等式直接证明
,利用基本不等式直接证明 .
.法二:通过
 ,以及0<an<1,说明
,以及0<an<1,说明 ,an∈[
,an∈[ ,1),n∈N*,构造函数
,1),n∈N*,构造函数 ,利用函数的导数,求出函数的最大值即可证明结果.
,利用函数的导数,求出函数的最大值即可证明结果.点评:本题考查数列与函数的综合应用,数学归纳法的证明方法,构造法以及函数的导数求解函数的最大值证明不等式,基本不等式的应用,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目