题目内容
已知函数f(x)的导数![]() 满足
满足![]() ,常数α为方程f(x)=x的实数根.
,常数α为方程f(x)=x的实数根.
(1).若函数f(x)的定义域为I,对任意![]() ,存在
,存在![]() ,使等式f(b)-f(a)=
,使等式f(b)-f(a)=![]() 成立,求证:方程f(x)=x不存在异于α的实数根;
成立,求证:方程f(x)=x不存在异于α的实数根;
(2).求证:当x>α时,总有f(x)<x成立;
(3).对任意x1,x2,若满足|x1-α|<1,|x2-α|<1,求证|f(x1)-f(x2)|<2.
答案:
解析:
解析:
|
(1).用反证法,设方程 由题意使等式 因为 因此,如若 (2).令 又 (3).不妨设 又 即 即 ∴ |

练习册系列答案
相关题目
 的图象如图所示,那么函数f (x)的图象最有可能的是( )
的图象如图所示,那么函数f (x)的图象最有可能的是( )
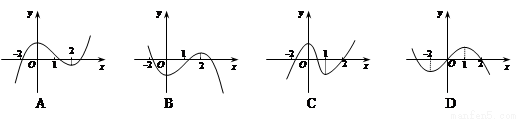
 ,且满足f(x)=2x
,且满足f(x)=2x +ln x,则
+ln x,则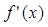 的图像如左图所示,那么函数f(x)的图像最有可能的
的图像如左图所示,那么函数f(x)的图像最有可能的