题目内容
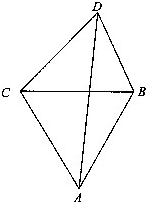 如图,我军某部军事演习时红方炮兵阵地位于A处,B,C是两雷达观察点,且B位于C正东与C距离为m,已知A与两雷达观察点B,C的距离也均为m,当绿方目标D出现在观察点B的北偏西15°和观察点C的北偏东45°交汇处时及时炮击,求炮击目标的距离AD(A,B,C,D在同一平面(地面)内).
如图,我军某部军事演习时红方炮兵阵地位于A处,B,C是两雷达观察点,且B位于C正东与C距离为m,已知A与两雷达观察点B,C的距离也均为m,当绿方目标D出现在观察点B的北偏西15°和观察点C的北偏东45°交汇处时及时炮击,求炮击目标的距离AD(A,B,C,D在同一平面(地面)内).分析:在△BCD中,求出∠BCD=45°、∠BDC=60°,利用正弦定理算出BD=
m,然后在△ABD中,∠ABD=∠ABC+∠CBD=135°,由余弦定理加以计算,即可算出AD长.
| ||
| 3 |
解答:解:在△BCD中,∠CBD=75°,∠BCD=45°,∠BDC=60°,BC=m
根据正弦定理
=
,
得BD=
=
=
m
又∵∠ABD=∠ABC+∠CBD=135°
∴在△ABD中,由余弦定理得
AD2=AB2+BD2-2AB•BDcos∠ABD
=m2+(
m)2-2×m×
m×cos135°=
m2,
∴AD=
m
答:炮击目标的距离AD等于
m.
根据正弦定理
| BC |
| sin∠BDC |
| BD |
| sin∠BCD |
得BD=
| BC•sin∠BCD |
| sin∠BDC |
| m•sin45° |
| sin60° |
| ||
| 3 |
又∵∠ABD=∠ABC+∠CBD=135°
∴在△ABD中,由余弦定理得
AD2=AB2+BD2-2AB•BDcos∠ABD
=m2+(
| ||
| 3 |
| ||
| 3 |
5-2
| ||
| 3 |
∴AD=
|
答:炮击目标的距离AD等于
|
点评:本题给出实际应用问题,求炮击目标的距离.着重考查了利用正余弦定理解三角形和解三角形的实际应用等知识点,属于中档题.

练习册系列答案
相关题目

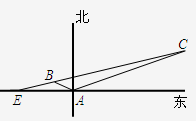 如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.
如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进. 如图,当输出S=1023时,(1)中应填的条件是( )
如图,当输出S=1023时,(1)中应填的条件是( ) 如图当参数λ=λ1、λ2时,连续函数
如图当参数λ=λ1、λ2时,连续函数