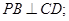题目内容
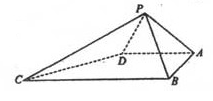
如图,在四棱锥P-ABCD中,PA丄平面ABCD, ,
,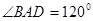 ,AD=AB=1,AC和BD交于O点.
,AD=AB=1,AC和BD交于O点.
(I)求证:平面PBD丄平面PAC.
(II)当点A在平面PBD内的射影G恰好是ΔPBD的重心时,求二面角B-PD-A的余弦值.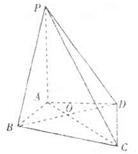
(Ⅰ)见解析;(II) 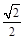 .
.
解析试题分析:(Ⅰ)利用条件证明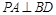 ,
,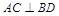 ,即可证平面
,即可证平面 平面
平面 ;(II)过
;(II)过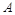 作
作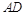 的垂线为
的垂线为 轴,
轴,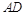 为
为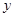 轴,
轴,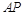 为
为 轴,建立空间坐标系,得各点坐标,设
轴,建立空间坐标系,得各点坐标,设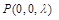 ,利用
,利用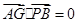 ,先求出
,先求出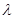 的值,再分别求面
的值,再分别求面 和面
和面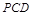 的法向量,从而可得结论.
的法向量,从而可得结论.
试题解析:(Ⅰ)依题意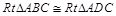 ,
,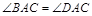 ,
,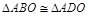 ,所以
,所以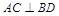 , 2分
, 2分
而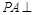 面
面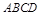 ,
,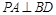 ,又
,又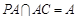 ,∴
,∴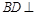 面
面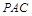 ,又
,又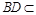 面
面 ,
,
∴平面 平面
平面 . 4分
. 4分
(Ⅱ)
过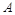 作
作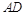 的垂线为
的垂线为 轴,
轴,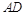 为
为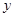 轴,
轴,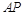 为
为 轴,建立如图所示坐标系,则
轴,建立如图所示坐标系,则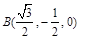 ,
,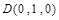 ,
, ,设
,设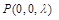 ,所以
,所以 ,
,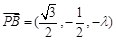 ,
,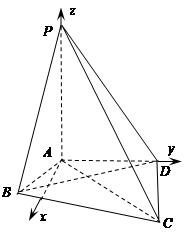
由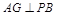 ,得
,得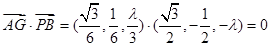
解得 ,
,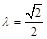 . 6分
. 6分
∴P点的坐标为 ;
;
面 的一个法向量为
的一个法向量为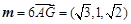 , 8分
, 8分
设面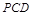 的一个法向量为
的一个法向量为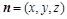 ,
,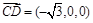 ,
,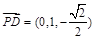
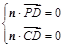 即
即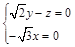 ,∴
,∴ , 10分
, 10分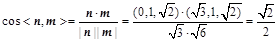 ,
,
所以二面角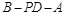 的余弦值为
的余弦值为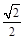 . 12分
. 12分
考点:1、面面垂直的判定定理;2、利用空间向量求二面角.

练习册系列答案
相关题目
 中,底面
中,底面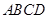 为平行四边形,侧面
为平行四边形,侧面 底面
底面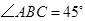 ,
,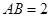 ,
,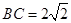 ,
,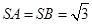 .
.
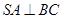 ;
;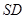 与平面
与平面 所成角的正弦值.
所成角的正弦值.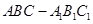 中,
中,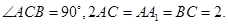

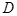 为
为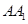 的中点,求证:平面
的中点,求证:平面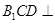 平面
平面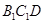 ;
;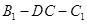 的大小为
的大小为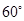 ,试确定
,试确定 中,
中,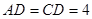 ,
, ,
, 是线段
是线段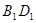 的中点.
的中点.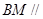 平面
平面 ;
;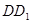 与平面
与平面
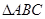 中,
中, ,
, ,
, 是
是 上的高,沿
上的高,沿 折起,使
折起,使 .
. ⊥平面
⊥平面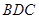 ;
;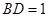 ,求三棱锥
,求三棱锥 的表面积.
的表面积.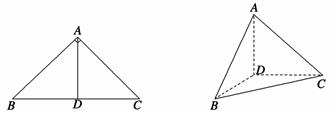
 中,
中,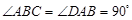 ,
,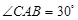 ,
,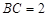 ,
,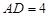 . 把
. 把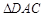 沿对角线
沿对角线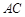 折起到
折起到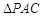 的位置,如图2所示,使得点
的位置,如图2所示,使得点 在平面
在平面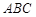 上的正投影
上的正投影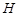 恰好落在线段
恰好落在线段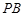 ,点
,点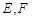 分别为线段
分别为线段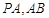 的中点.
的中点. 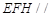 平面
平面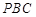 ;
;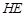 与平面
与平面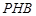 所成角的正弦值;
所成角的正弦值;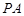 上是否存在一点
上是否存在一点 ,使得
,使得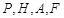 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.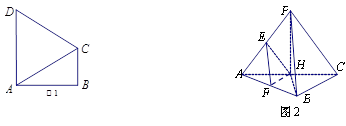
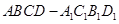 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱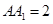 ,
,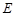 为
为 中点,
中点,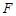 为
为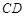 中点,
中点,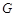 为
为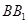 上一个动点.
上一个动点.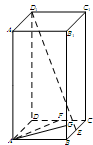
 ;
;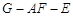 的平面角余弦值.
的平面角余弦值.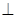 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.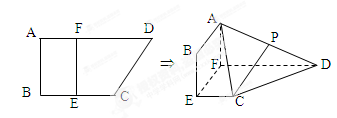
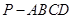 中,
中,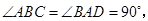
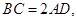
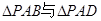 都是边长为
都是边长为 的等边三角形.
的等边三角形.