题目内容
如图,在直三棱柱(即侧棱与底面垂直的三棱柱)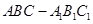 中,
中,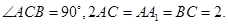

(I)若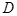 为
为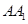 的中点,求证:平面
的中点,求证:平面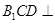 平面
平面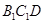 ;
;
(II)若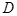 为线段
为线段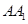 上一点,且二面角
上一点,且二面角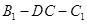 的大小为
的大小为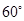 ,试确定
,试确定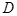 的位置.
的位置.
(I)略;(II) .
.
解析试题分析:(I)可以转为证线面垂直或利用空间向量证明面面垂直;(II)可利用 的面积求
的面积求 也可利用空间向量求
也可利用空间向量求 .
.
试题解析:方法一:(I)证明:∵ ,∴
,∴ .
. 
又由直三棱柱的性质知 ,
, 
∴ 平面
平面 ,∴
,∴ , ①
, ①
由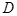 为
为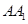 的中点,可知
的中点,可知 ,
,
∴ ,即
,即 , ②
, ②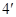
又 ③
③
由①②③可知 平面
平面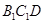 ,
, 
又 平面
平面 ,故平面
,故平面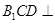 平面
平面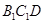 .
. 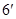
(II)解:由(I)可知 平面
平面 ,在平面
,在平面 内过
内过 作
作 ,交
,交 或其延长线于
或其延长线于 ,连接
,连接 ,∴
,∴ 为二面角
为二面角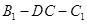 的平面角,
的平面角, 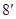
∴ .由
.由 知,
知, ,设
,设 ,则
,则 .
.
∵ 的面积为
的面积为 ,∴
,∴ .
. 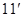
解得 ,即
,即 .
. 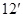

方法二:(I)证明:如图,以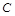 为坐标原点,
为坐标原点, 所在的直线分别为
所在的直线分别为 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 即
即

由 ,得
,得 ;
; 
同理可证 ,得
,得 .
. 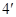
又 平面
平面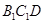 .
. 
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
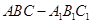 中,点
中,点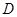 是
是 的中点.
的中点.
 平面
平面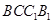 ;
; 平面
平面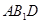 .
.
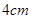 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为 ,构成一个三棱锥.
,构成一个三棱锥.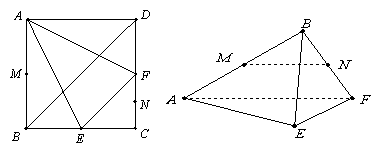
 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 平面
平面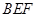 ;
;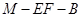 的余弦值.
的余弦值.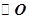 的直径,D为
的直径,D为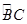 的中点,E为BC的中点.
的中点,E为BC的中点.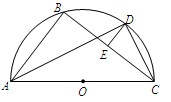
 是矩形
是矩形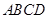 中
中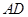 边上的点,
边上的点, 为
为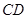 边的中点,
边的中点,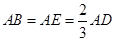 ,现将
,现将 沿
沿 边折至
边折至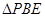 位置,且平面
位置,且平面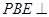 平面
平面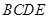 .
. 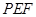 ;
;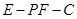 的大小.
的大小. 
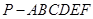 的底面是边长为1的正六边形,
的底面是边长为1的正六边形,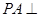 底面
底面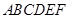 。
。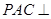 平面
平面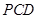 ;
;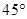 ,求三棱锥
,求三棱锥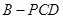 高的大小。
高的大小。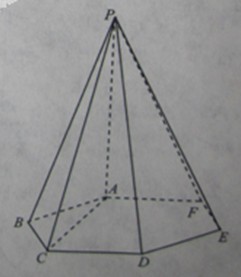
 ,
, ,AD=AB=1,AC和BD交于O点.
,AD=AB=1,AC和BD交于O点.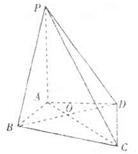
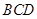 是等边三角形,
是等边三角形, 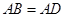 ,
,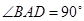 ,
,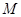 ,
, ,
,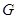 分别是
分别是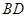 ,
,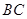 ,
, 的中点,将△
的中点,将△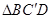 的位置,使得
的位置,使得 .
.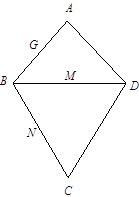

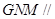 平面
平面 ;
;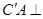 平面
平面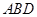 .
.