题目内容

已知函数 $数学公式$ 的图象过点 $数学公式$ ．
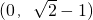（1）求f（x）的解析式；
（2）设P₁（x₁，y₁），P₂（x₂，y₂）为y=f（x）的图象上两个不同点，又点P（x_P，y_P）满足： $数学公式$ ，其中O为坐标原点．试问：当 $数学公式$ 时，y_P是否为定值？若是，求出y_P的值，若不是，请说明理由．

解：（1）由题意知 $\text{[math]}$ ，
解得a=1，
∴ $\text{[math]}$ ；
（2） $\text{[math]}$ $\text{[math]}$
= $\text{[math]}$
= $\text{[math]}$ ，
∴y_p为定值 $\text{[math]}$ ．
分析：（1）由题意知 $\text{[math]}$ ，解得a=1，由此能求出f（x）的解析式．
（2） $\text{[math]}$ ，由此能够推导出y_p为定值 $\text{[math]}$ ．
点评：本题考查函数解析式的常用解法，解题时要认真审题，仔细解答，注意合理地进行等价转化．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

（05年福建卷文）（12分）

已知函数的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为.

（Ⅰ）求函数的解析式；

（Ⅱ）求函数的单调区间.

（本小题满分13分）

已知函数的图象过点，且在点处的切线方程为.

（Ⅰ）求函数的解析式；

（Ⅱ）求函数的单调区间.

的图象过点A（3，7），则此函的最小值是．

（本小题满分12分）

已知函数的图象过点，且图象上与点P最近的一个最低点是．

（Ⅰ）求的解析式；

（Ⅱ）若，且为第三象限的角，求的值；

（Ⅲ）若在区间上有零点，求的取值范围．

已知函数的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为.

（1）求函数的解析式；（2）求函数的单调区间