题目内容
已知函数 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
.
(1)求函数 的解析式; (2)求函数
的解析式; (2)求函数 的单调区间
的单调区间
【答案】
解:(Ⅰ)由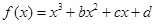 的图象过点P(0, 2),d=2知,所以
的图象过点P(0, 2),d=2知,所以 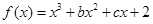 ,
,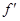 (x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知-6-f(-1)+7=0,即f(-1)=1,
(x)=3x2+2bx+c,由在(-1,(-1))处的切线方程是6x-y+7=0,知-6-f(-1)+7=0,即f(-1)=1, 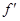 (-1)=6,∴
(-1)=6,∴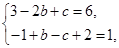 即
即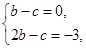 解得b=c=-3.故所求的解析式为f(x)=x3-3x2-3x+2,
解得b=c=-3.故所求的解析式为f(x)=x3-3x2-3x+2,
(Ⅱ) 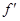 (x)=3x2-6x-3,令3x2-6x-3=0即x2-2x-1=0,解得x1=1-
(x)=3x2-6x-3,令3x2-6x-3=0即x2-2x-1=0,解得x1=1-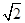 ,x2=1+
,x2=1+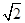 ,
,
当x<1-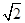 或x>1+
或x>1+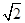 时,
时, 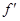 (x)>0;当1-
(x)>0;当1-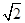 <x<1+
<x<1+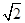 时,
时, 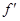 (x)<0
(x)<0
∴f(x)=x3-3x2-3x+2的单调递增区间为(1+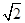 ,+∞)和(-∞, 1-
,+∞)和(-∞, 1-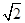 ),单调递减区间为(1-
),单调递减区间为(1-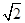 ,1+
,1+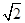 ).
).
【解析】略

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
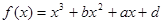 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为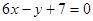 .
.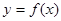 的解析式;
的解析式;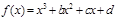 的图象过点P(0,2),且在点
的图象过点P(0,2),且在点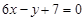 .求函数y=f(x)的解析式;
.求函数y=f(x)的解析式;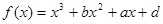 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M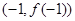 处的切线方程为
处的切线方程为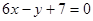 .
.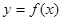 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数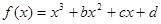 的图象过点P
的图象过点P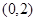 ,
且在点M
,
且在点M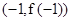 处的切线方程为
处的切线方程为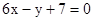 .
.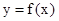 的解析式; (2) 求函数
的解析式; (2) 求函数