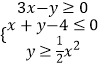Question

【题目】△ABC的三个内角A，B，C的对边分别a，b，c，已知 ， ，且 ∥
（1）证明sinBsinC=sinA；
（2）若a2+c2﹣b2= ac，求tanC．

Answer 1

【答案】
（1）证明：由 ， ，且 ∥ ，

可得 = + ，

由正弦定理可得 = + =1，

即有sinBcosC+cosBsinC=sinBsinC，

即为sin（B+C）=sinBsinC，

则sinBsinC=sinA；

（2）由（1） + =1，

可得tanB+tanC=tanBtanC，

由a2+c2﹣b2= ac，

由余弦定理可得，cosB= = = ，

sinB= = ，

可得tanB= = ，

则tanC= = =

【解析】（1）运用向量共线的坐标表示，结合正弦定理和两角和的正弦公式，化简整理即可得证；（2）运用余弦定理和同角的基本关系式，计算即可得到所求值．