题目内容
如图,设抛物线 :
: 的焦点为
的焦点为 ,准线为
,准线为 ,过准线
,过准线 上一点
上一点 且斜率为
且斜率为 的直线
的直线 交抛物线
交抛物线 于
于 ,
, 两点,线段
两点,线段 的中点为
的中点为 ,直线
,直线 交抛物线
交抛物线 于
于 ,
, 两点.
两点.
(1)求抛物线 的方程及
的方程及 的取值范围;
的取值范围;
(2)是否存在 值,使点
值,使点 是线段
是线段 的中点?若存在,求出
的中点?若存在,求出 值,若不存在,请说明理由.
值,若不存在,请说明理由. 
(1)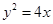 ,
,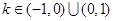 ;(2)不存在.参考解析
;(2)不存在.参考解析
解析试题分析:(1)由准线 上一点
上一点 ,所以可以求得
,所以可以求得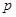 的值,即可取得抛物线的方程.由于直线与抛物线有两个交点,所以联立方程消去y,需要判别式大于零即可得到k的取值范围,又由于k等于零时没有两个交点,所以应排除,即可得到结论.
的值,即可取得抛物线的方程.由于直线与抛物线有两个交点,所以联立方程消去y,需要判别式大于零即可得到k的取值范围,又由于k等于零时没有两个交点,所以应排除,即可得到结论.
(2)是否存在 值,使点
值,使点 是线段
是线段 的中点.由直线AB的方程联立抛物线的方程,即可求得AB中点P的坐标.从而写出PF的方程再联立抛物线的方程,对比DE的中点是否与AB的中点相同.即可得到答案.
的中点.由直线AB的方程联立抛物线的方程,即可求得AB中点P的坐标.从而写出PF的方程再联立抛物线的方程,对比DE的中点是否与AB的中点相同.即可得到答案.
(1)由已知得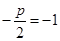 ,∴
,∴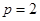 .∴抛物线方程为
.∴抛物线方程为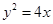 . 2分
. 2分
设 的方程为
的方程为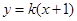 ,
,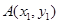 ,
,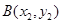 ,
,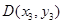 ,
,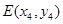 ,
,
由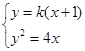 得
得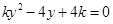 . 4分
. 4分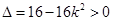 ,解得
,解得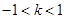 ,注意到
,注意到 不符合题意,
不符合题意,
所以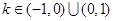 . 5分
. 5分
(2)不存在 值,使点
值,使点 是线段
是线段 的中点.理由如下: 6分
的中点.理由如下: 6分
有(1)得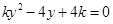 ,所以
,所以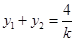 ,所以
,所以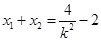 ,
,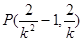 ,直线
,直线 的方程为
的方程为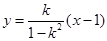 . 8分
. 8分
由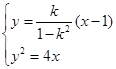 得
得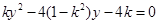 ,
,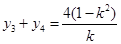 . 10分
. 10分
当点 为线段
为线段 的中点时,有
的中点时,有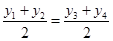 ,即
,即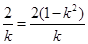 ,因为
,因为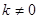 ,所以此方程无实数根.因此不存在
,所以此方程无实数根.因此不存在 值,使点
值,使点 是线段
是线段 的中点. 12分
的中点. 12分
考点:1.抛物线的性质.2.联立方程解方程组的思想.3.存在性的问题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 (
(  )的离心率为
)的离心率为 ,点(1,
,点(1, )在椭圆C上.
)在椭圆C上. ),其中
),其中 ,切点分别是A、B,试利用结论:在椭圆
,切点分别是A、B,试利用结论:在椭圆 )处的椭圆切线方程是
)处的椭圆切线方程是 ,证明直线AB恒过椭圆的右焦点
,证明直线AB恒过椭圆的右焦点 ;
; 的值是否恒为常数,若是,求出此常数;若不是,请说明理由.
的值是否恒为常数,若是,求出此常数;若不是,请说明理由. 的离心率
的离心率 ,
, .
.
 是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交
是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交 轴于点N,直线AD交BP于点M。设BP的斜率为
轴于点N,直线AD交BP于点M。设BP的斜率为 ,MN的斜率为
,MN的斜率为 .证明:
.证明: 为定值。
为定值。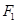 、
、 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点 为其上一点,且有
为其上一点,且有
 .
. 的标准方程;
的标准方程; 与椭圆
与椭圆 交于
交于 、
、 两点,过
两点,过 与椭圆
与椭圆 两点,求四边形
两点,求四边形 的面积
的面积 的最大值.
的最大值.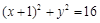 ,点
,点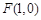 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.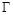 的方程;
的方程; ,
, ,点G是轨迹
,点G是轨迹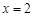 相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.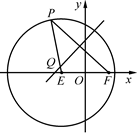
 ,
, ,
, ,
, 分别是椭圆
分别是椭圆 的四个顶点,△
的四个顶点,△ 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆 .
. 及圆
及圆 的方程;
的方程; 是圆
是圆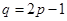 劣弧
劣弧 上一动点(点
上一动点(点 ,
, ),直线
),直线 分别交线段
分别交线段 ,椭圆
,椭圆 与
与 交于点
交于点 .
. 的最大值;
的最大值; ,
, 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
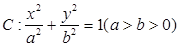 ,过点
,过点 且离心率为
且离心率为 .
. 的方程;
的方程; 是椭圆
是椭圆 满足
满足 ,连接
,连接 角椭圆于点
角椭圆于点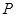 ,在
,在 轴上是否存在异于点
轴上是否存在异于点 ,使得以
,使得以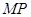 为直径的圆经过直线
为直径的圆经过直线 和直线
和直线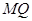 的交点,若存在,求出
的交点,若存在,求出
 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 ,过
,过 的直线与曲线
的直线与曲线 ,过
,过 的直线与曲线
的直线与曲线 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 ,设点
,设点 (
( ).
). ,并求
,并求 与
与 的关系式(
的关系式( (
( ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由; ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论. 轴上的椭圆过点
轴上的椭圆过点 ,且它的离心率
,且它的离心率 .
.
 相切的直线
相切的直线 交椭圆于
交椭圆于 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.