题目内容
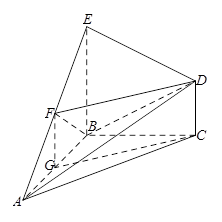
如图,在几何体 中,
中, 平面
平面 ,
,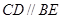 ,
,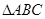 是等腰直角三角形,
是等腰直角三角形,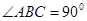 ,且
,且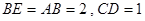 ,点
,点 是
是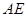 的中点.
的中点.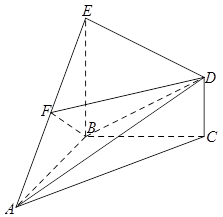
(Ⅰ)求证: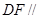 平面
平面 ;
;
(Ⅱ)求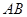 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(Ⅰ)详见解析;(Ⅱ)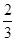 .
.
解析试题分析:(Ⅰ)证法一是取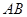 的中点
的中点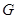 ,构造四边形
,构造四边形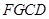 ,并证明四边形
,并证明四边形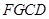 为平行四边形,得到
为平行四边形,得到 ,从而证明
,从而证明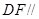 平面
平面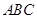 ;证法二是取
;证法二是取 的中点
的中点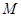 ,构造平面
,构造平面 ,通过证明平面
,通过证明平面 平面
平面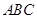 ,并利用平面与平面平行的性质来证明
,并利用平面与平面平行的性质来证明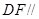 平面
平面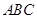 ;(Ⅱ)直接利用空间向量法求直线
;(Ⅱ)直接利用空间向量法求直线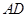 与平面
与平面 所成角的正弦值.
所成角的正弦值.
试题解析:解法一:(Ⅰ)取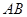 的中点
的中点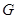 ,连结
,连结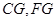 ,
,
则 ,且
,且 , 2分
, 2分
又 ,∴
,∴ 且
且 ,所以四边形
,所以四边形 是平行四边形,
是平行四边形,
则 , 5分
, 5分
又因为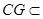 平面
平面 ,
, 平面
平面 ,所以
,所以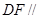 平面
平面 . 6分
. 6分
(Ⅱ)依题得,以点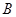 为原点,
为原点, 所在的直线分别为
所在的直线分别为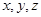 轴,建立如图的空间直角坐标系,
轴,建立如图的空间直角坐标系,
则 ,
, ,
,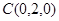 ,
, ,
,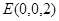 ,
,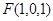 ,
,
所以 ,
,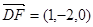 .
.
设平面 的一个法向量为
的一个法向量为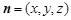 ,则
,则 即
即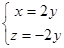 ,
,
取 ,得,
,得, . 10分
. 10分
又设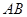 与平面
与平面 所成的角为
所成的角为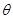 ,
, ,
,
则 ,
,
故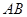 与平面
与平面 所成角的正弦值为
所成角的正弦值为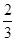 . 13分
. 13分
解法二:(Ⅰ)取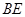 的中点
的中点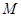 ,连结
,连结 ,
,
则 ,
,
又因为 平面
平面 ,
,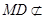 平面
平面 ,
, 平面
平面

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中, ,点
,点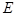 是
是 的中点.
的中点.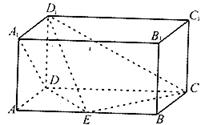
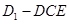 的体积;
的体积; ;
; 的正切值.
的正切值.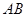 为圆
为圆 的直径,点
的直径,点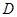 为线段
为线段 ,点
,点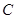 为圆
为圆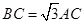 .点
.点 在圆
在圆 .
.
 ;
; 的余弦值.
的余弦值. 所在平面与直角梯形
所在平面与直角梯形 所在平面互相垂直,
所在平面互相垂直, ,
, 点
点 分别是线段
分别是线段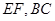 的中点.
的中点. 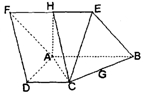

 平面
平面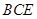 ;
; 在直线
在直线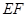 上,且
上,且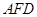 ,求平面
,求平面 与平面
与平面 所成角的余弦值。
所成角的余弦值。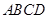 中,
中,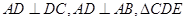 是边长为2的等边三角形,
是边长为2的等边三角形,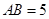 .沿
.沿 将
将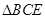 折起,使
折起,使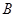 至
至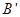 处,且
处,且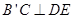 ;然后再将
;然后再将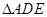 沿
沿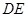 折起,使
折起,使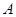 至
至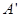 处,且面
处,且面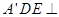 面
面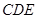 ,
,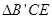 和
和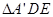 在面
在面

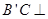 平面
平面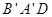 与平面
与平面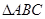 中,
中, ,
, ,
, 是
是 上的高,沿
上的高,沿 折起,使
折起,使 .
. ⊥平面
⊥平面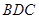 ;
;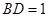 ,求三棱锥
,求三棱锥 的表面积.
的表面积.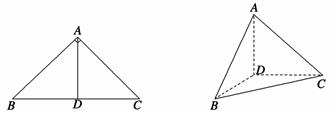
 中,
中, ,
, ,
, ,设顶点A在底面
,设顶点A在底面 上的射影为R.
上的射影为R.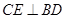 ;
; 在棱
在棱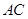 上,且
上,且 ,试求二面角
,试求二面角 的余弦值.
的余弦值.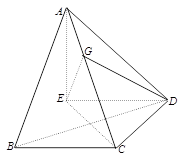
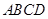 的4个顶点都在球
的4个顶点都在球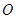 的表面上,
的表面上,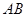 为球
为球 为球面上一点,且
为球面上一点,且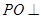 平面
平面 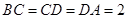 ,点
,点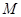 为
为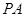 的中点.
的中点. 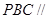 平面
平面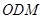 ;
; 与平面
与平面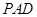 所成锐二面角的余弦值.
所成锐二面角的余弦值.
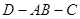 ,如图二,在二面角
,如图二,在二面角