题目内容
已知命题p：四边形确定一个平面，命题q：两两相交的三条直线确定一个平面，则下列命题为真命题的是（ ）
| A、p∧q | B、p∨q |
| C、（￢p）∨q | D、p∧（￢q） |
考点：复合命题的真假
专题：简易逻辑
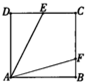
分析：命题p：是一个假命题，例如：把一个平面四边形沿着对角线折起一个角度可得一个空间四边形；
命题q：是一个假命题，例如一个三棱锥的三条棱不在同一个平面内．
命题q：是一个假命题，例如一个三棱锥的三条棱不在同一个平面内．
解答：
解：命题p：四边形确定一个平面，是一个假命题，例如：把一个平面四边形沿着对角线折起一个角度可得一个空间四边形，因此不正确；
命题q：两两相交的三条直线确定一个平面，是一个假命题，例如一个三棱锥的三条棱不在同一个平面内．
因此￢p∨q是真命题．
故选：C．
命题q：两两相交的三条直线确定一个平面，是一个假命题，例如一个三棱锥的三条棱不在同一个平面内．
因此￢p∨q是真命题．
故选：C．
点评：本题考查了简易逻辑的判定、空间线面的位置关系判定，考查了推理能力，属于基础题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
函数y=sin2x的图象经过变换得到y=sin（2x+
）的图象，则该变换可以是（ ）
| π |
| 3 |
A、所有点向右平移
| ||
B、所有点向左平移
| ||
C、所有点向左平移
| ||
D、所有点向右平移
|