题目内容
已知函数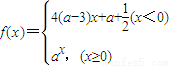
，若函数f（x）的图象经过点（3，
），则a= ；若函数f（x）满足对任意x1≠x2，
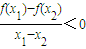都有成立，那么实数a的取值范围是 ．
【答案】分析：函数f（x）的图象经过点（3，
），因为3＞0，故
，可求出a；
函数f（x）满足对任意x1≠x2，
，即f（x）为减函数，只要考虑x＜0时的单调性即可．
解答：解：函数f（x）的图象经过点（3，
），因为3＞0，故
，所以a=
；
函数f（x）满足对任意x1≠x2，
，即f（x）为减函数，
x≥0时，f（x）=ax为减函数，则0＜a＜1，且f（0）=1，
x＜0时，f（x）=4（a-3）x+a+
为减函数，故a-3＜0，a＜3，且x→0时，f（x）→
≥f（0）=1，所以
综上可得：
故答案为：
，
点评：本题考查待定系数法求函数解析式、分段函数的单调性，难度一般．
），因为3＞0，故，可求出a；函数f（x）满足对任意x1≠x2，
，即f（x）为减函数，只要考虑x＜0时的单调性即可．解答：解：函数f（x）的图象经过点（3，
），因为3＞0，故，所以a=；函数f（x）满足对任意x1≠x2，
，即f（x）为减函数，x≥0时，f（x）=ax为减函数，则0＜a＜1，且f（0）=1，
x＜0时，f（x）=4（a-3）x+a+
为减函数，故a-3＜0，a＜3，且x→0时，f（x）→≥f（0）=1，所以综上可得：
故答案为：
，点评：本题考查待定系数法求函数解析式、分段函数的单调性，难度一般．
练习册系列答案
阅读快车系列答案
相关题目