题目内容
已知函数
(1)求函数 的值域,并写出函数
的值域,并写出函数 的单调递增区间;
的单调递增区间;
(2)若 ,且
,且 ,计算
,计算 的值.
的值.
【答案】
(1)值域为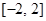 ;单调递增区间为
;单调递增区间为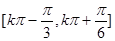 ,
,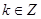 (2)
(2)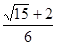 .
.
【解析】
试题分析:(1)本小题首先需要对函数解析式进行化简变形得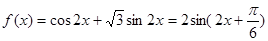 ,然后根据
,然后根据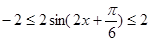 求得函数
求得函数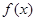 的值域为
的值域为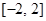 ;由
;由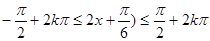 得
得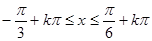 ,所以函数
,所以函数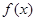 的单调递增区间为
的单调递增区间为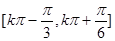 ,
,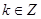 ;
;
(2)本小题首先根据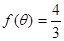 代入可得
代入可得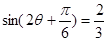 ,利用
,利用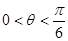 可判断
可判断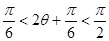 ,于是求得
,于是求得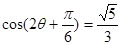 ,然后
,然后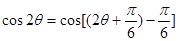 展开代入求值即可.
展开代入求值即可.
试题解析:(1)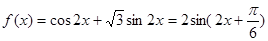 2分
2分
由于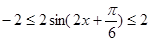 ,所以函数
,所以函数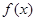 的值域为
的值域为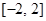 4分
4分
由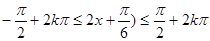 得
得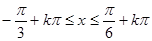
所以函数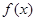 的单调递增区间为
的单调递增区间为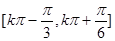 ,
,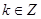 6分
6分
(2)由(1)得,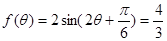 ,即
,即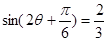 8分
8分
其中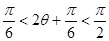 得
得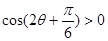 10分
10分
所以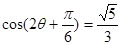 11分
11分
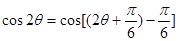 13分
13分
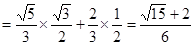 14分
14分
考点:1.三角恒等变换;2.正弦曲线的图像与性质.

练习册系列答案
相关题目
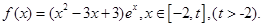
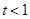 时,求函数
时,求函数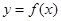 的单调区间;
的单调区间;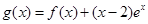 ,试问函数
,试问函数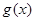 在
在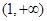 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1.
 ,
, ,
, ,
, 这几个函数值,你能发现f(x)与
这几个函数值,你能发现f(x)与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;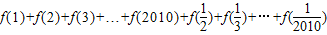 的值;
的值; 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性.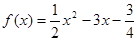
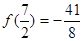 ,求
,求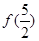
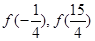 的大小
的大小