题目内容
O为△ABC内一点，
=λ
+μ
，则λ+2μ的取值范围 ．
| AO |
| AB |
| AC |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：B连接AC中点D，并设AO所在直线交BD于E点，
=k
=λ
+2μ
，因为B，E，D三点共线，所以便有
+
=1，所以得到λ+2μ=k，显然k＞0，并且O趋向C时，k逐渐增大，当O与C重合时k=2，所以0＜k＜2．
| AO |
| AE |
| AB |
| AD |
| λ |
| k |
| 2μ |
| k |
解答：
解：如图，取AC中点D，并连接BD，设AO所在直线和BD交于E，并设
=k
；
∴k
=λ
+2μ
；
∴
=
+
；
∵B，D，E三点共线；
∴
+
=1；
∴λ+2μ=k；
∵O在△ABC内；
∴k＞0，而当O趋向于C点时，k不断增大，且k趋向2；
∴0＜k＜2；
∴λ+2μ的取值范围为（0，2）．
故答案为：（0，2）．
解：如图，取AC中点D，并连接BD，设AO所在直线和BD交于E，并设| AO |
| AE |
∴k
| AE |
| AB |
| AD |
∴
| AE |
| λ |
| k |
| AB |
| 2μ |
| k |
| AD |
∵B，D，E三点共线；
∴
| λ |
| k |
| 2μ |
| k |
∴λ+2μ=k；
∵O在△ABC内；
∴k＞0，而当O趋向于C点时，k不断增大，且k趋向2；
∴0＜k＜2；
∴λ+2μ的取值范围为（0，2）．
故答案为：（0，2）．
点评：考查共线向量基本定理，当A，B，C三点共线时，若
=λ
+μ
，则λ+μ=1，要弄清O点的位置和k的取值的关系．
| OB |
| OA |
| OC |
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
已知直线ax+y+2=0的倾斜角为
，则a等于（ ）
| 3π |
| 4 |
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、-2 |
如图所示，是一个空间几何体的三视图，则这个空间几何体是（ ）
| A、长方体 | B、球 | C、圆锥 | D、圆柱 |
如图，M是三棱锥P-ABC的底面△ABC的重心，若
=x
+y
+z
，则x+y-z的值为（ ）
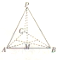
| PM |
| PA |
| PB |
| PC |
A、
| ||
B、
| ||
C、
| ||
| D、1 |