题目内容
10.关于定义在R上的函数f(x),给出下列三个命题①若f(1)=f(-1),则f(x)不是奇函数;
②若f(1)>f(-1),则f(x)在R上不是单调减函数;
③若f(1+x)=f(x-1)对任意的x∈R恒成立,则f(x)是周期函数.
其中所有正确的命题序号是②③.
分析 结合函数的奇偶性,函数的单调性,函数的周期性的定义,逐一分析三个结论的真假,可得答案.
解答 解:定义在R上的函数f(x),
①若f(1)=f(-1)=0,则f(x)可能是奇函数,故错误;
②若f(1)>f(-1),则f(x)在R上不是单调减函数,故正确;
③若f(1+x)=f(x-1)对任意的x∈R恒成立,则f(x+2)=f(x),则f(x)是周期函数,故正确.
故正确的命题为:②③,
故答案为:②③
点评 本题以命题的真假判断与应用为载体,考查了函数的奇偶性,函数的单调性,函数的周期性,难度中档.

练习册系列答案
相关题目
20.已知平面向量$\overrightarrow a,\overrightarrow b$为单位向量,$|\overrightarrow a+\overrightarrow b|=1$,则向量$\overrightarrow a,\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
5.如图程序中,若输入x=-2,则输出y的值为( )
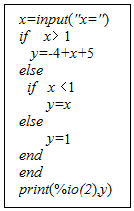
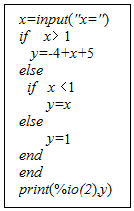
| A. | 1 | B. | 13 | C. | -2 | D. | -3 |
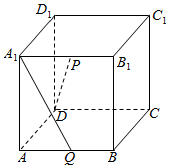 如图,在正方体ABCD-A1B1C1D1中,P是A1B1的中点,Q是AB的中点,求异面直线A1Q与DP所成角的余弦值.
如图,在正方体ABCD-A1B1C1D1中,P是A1B1的中点,Q是AB的中点,求异面直线A1Q与DP所成角的余弦值.