题目内容
【题目】已知函数![]() .
.
(1)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同的解
上有两个不同的解![]() .
.
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)设函数![]() 在区间
在区间![]() 上的最大值和最小值分别为
上的最大值和最小值分别为![]() ,求
,求![]() 的表达式.
的表达式.
【答案】(1)(i)![]() ;(ii)
;(ii)![]() ;
;
(2)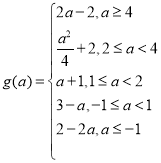 .
.
【解析】
试题分析:(1)借助题设条件运用函数的图象和不等式的性质求解;(2)借助题设运用函数的性质和分类整合思想探求.
试题解析:
(1)由![]() ,
,![]()
得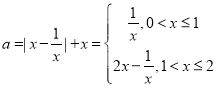 ,
,
(ⅰ)作出函数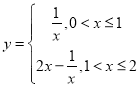 图象,得
图象,得![]() ,
,
故![]() 的取值范围是
的取值范围是![]() .
.
(ⅱ)∵![]() ,
,![]() ,
,![]() ,
,
则有![]() ,即
,即![]() ,
,
又![]() ,∴
,∴![]() ,
,
故![]() 的取值范围是
的取值范围是![]() .
.
(2)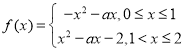 ,
,
当![]() 时,有
时,有![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,
则![]() .
.
当![]() 时,有
时,有![]() ,
,![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
此时![]() ,
,![]() ,
,
则![]() .
.
当![]() 时,有
时,有![]() ,
,![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
此时,![]() ,
,![]() ,
,
则![]() .
.
当![]() 时,有
时,有![]() ,
,![]() ,
,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
此时![]() ,
,
![]() ,
,
则![]() .
.
当![]() 时,有
时,有![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
则![]() .
.
则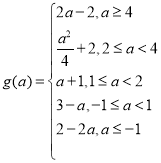

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目