题目内容
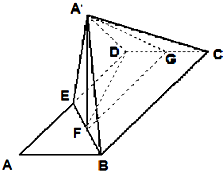 (2012•珠海一模)矩形ABCD中,2AB=AD=4,E是AD中点,沿BE将△ABE折起到△A′BE的位置,使A′C=A′D,F、G分别是BE、CD中点.
(2012•珠海一模)矩形ABCD中,2AB=AD=4,E是AD中点,沿BE将△ABE折起到△A′BE的位置,使A′C=A′D,F、G分别是BE、CD中点.(1)求证:A′F⊥CD;
(2)几何体A′-BCDE的体积.
分析:(1)利用线面垂直的性质:先证明CD⊥FG,CD⊥A′G,从而可证明CD⊥平面A′FG,由此可得A′F⊥CD;
(2)利用锥体的体积公式求:在△A′EF中,用勾股定理可得A′F,由梯形面积公式可得S四边形BCDE,从而有锥体的体积公式可得答案;
(2)利用锥体的体积公式求:在△A′EF中,用勾股定理可得A′F,由梯形面积公式可得S四边形BCDE,从而有锥体的体积公式可得答案;
解答:证明:(1)因为F、G分别是BE、CD的中点,所以FG∥BC,所以FG⊥CD,
因为A′C=A′D,所以A′G⊥CD,
又FG∩A′G=G,所以CD⊥平面A′GF,
所以CD⊥A′F.
(2)由(1)知CD⊥A′F,
又A′E=A′B,F为BE中点,所以A′F⊥BE,
所以A′F⊥平面BCDE,
A′E=2,EF=
EB=
,所以A′F=
=
,
所以几何体A′-BCDE的体积VA-BCDE=
A′F•S四边形BCDE=
•
•
•2=2
.
因为A′C=A′D,所以A′G⊥CD,
又FG∩A′G=G,所以CD⊥平面A′GF,
所以CD⊥A′F.
(2)由(1)知CD⊥A′F,
又A′E=A′B,F为BE中点,所以A′F⊥BE,
所以A′F⊥平面BCDE,
A′E=2,EF=
| 1 |
| 2 |
| 2 |
22-(
|
| 2 |
所以几何体A′-BCDE的体积VA-BCDE=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2+4 |
| 2 |
| 2 |
点评:本题考查线面垂直的判定、性质,考查锥体的体积公式,考查学生的逻辑推理能力,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
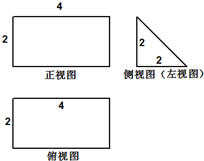 (2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( )
(2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( ) (2012•珠海一模)如图,在△ABC中,已知
(2012•珠海一模)如图,在△ABC中,已知