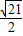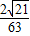题目内容
已知PA垂直于矩形ABCD所在平面,PA=3,AB=2,BC=
,则二面角P-BD-A的正切值为( )
| 3 |
| A、1 | ||||
| B、2 | ||||
C、
| ||||
D、
|
分析:因为PA⊥面ABCD,所以由三垂线定理法做二面角,过A做AH⊥BD与H,连接PH即可,再在直角△PHB中求解.
解答:解:过A做AH⊥BD与H,连接PH,因为PA⊥面ABCD,所以∠PHA即为二面角P-BD-A的平面角.
在直角△PHB中,因为PA=3,AH=
=
=
,
所以tan∠PHA=
=
=
故选C
在直角△PHB中,因为PA=3,AH=
| AB×AD |
| BD |
2
| ||
|
2
| ||
| 7 |
所以tan∠PHA=
| PA |
| AH |
| 3 | ||||
|
| ||
| 2 |
故选C
点评:本题考查三垂线定理法求二面角,考查运算能力.

练习册系列答案
相关题目
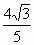 ,则二面角A
,则二面角A BD
BD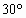
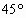
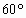
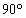
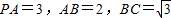 ,则二面角P-BD-A的正切值为( )
,则二面角P-BD-A的正切值为( )