题目内容
已知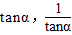 是关于x的方程
是关于x的方程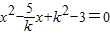 的两个实根,且
的两个实根,且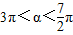 ,cosα+sinα= .
,cosα+sinα= .
【答案】分析:由根与系数关系可得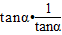 =k2-3=1,解之可得k值,由α所在象限可得tanα>0,进而可得
=k2-3=1,解之可得k值,由α所在象限可得tanα>0,进而可得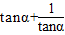 =
=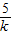 =
= ,化简可得tanα的方程,解之结合同角三角函数的基本关系可解得
,化简可得tanα的方程,解之结合同角三角函数的基本关系可解得
cosα和sinα的值,进而可得答案.
解答:解:由题意可得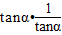 =k2-3=1,解得k=±2,
=k2-3=1,解得k=±2,
而3π<α< π可推得2π+π<α<2π+
π可推得2π+π<α<2π+ π,
π,
故α为第三象限角∴tanα>0,
∴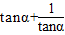 >0,∴
>0,∴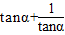 =
=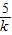 =
= ,
,
化简可得2tan2α-5tanα+2=0,解得tanα=2,或tanα= ,
,
当tanα=2时,由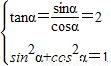 可解得sinα=
可解得sinα=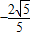 ,cosα=
,cosα=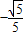 ,
,
当tanα= 时,由
时,由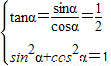 可解得sinα=
可解得sinα=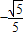 ,cosα=
,cosα=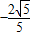 ,
,
故可得cosα+sinα=-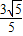 ,
,
故答案为:-
点评:本题考查同角三角函数的基本关系,以及一元二次方程根与系数的关系,属基础题.
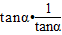 =k2-3=1,解之可得k值,由α所在象限可得tanα>0,进而可得
=k2-3=1,解之可得k值,由α所在象限可得tanα>0,进而可得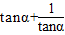 =
=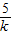 =
= ,化简可得tanα的方程,解之结合同角三角函数的基本关系可解得
,化简可得tanα的方程,解之结合同角三角函数的基本关系可解得cosα和sinα的值,进而可得答案.
解答:解:由题意可得
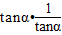 =k2-3=1,解得k=±2,
=k2-3=1,解得k=±2,而3π<α<
 π可推得2π+π<α<2π+
π可推得2π+π<α<2π+ π,
π,故α为第三象限角∴tanα>0,
∴
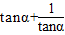 >0,∴
>0,∴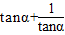 =
=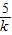 =
= ,
,化简可得2tan2α-5tanα+2=0,解得tanα=2,或tanα=
 ,
,当tanα=2时,由
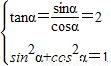 可解得sinα=
可解得sinα=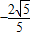 ,cosα=
,cosα=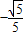 ,
,当tanα=
 时,由
时,由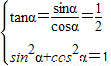 可解得sinα=
可解得sinα=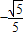 ,cosα=
,cosα=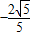 ,
,故可得cosα+sinα=-
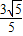 ,
,故答案为:-

点评:本题考查同角三角函数的基本关系,以及一元二次方程根与系数的关系,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是关于x的方程
是关于x的方程 的两个实根,且
的两个实根,且 ,cosα+sinα=________.
,cosα+sinα=________. 是关于x的方程
是关于x的方程 的两个实根,且
的两个实根,且 ,求
,求 的值.
的值.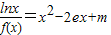 的根的个数.
的根的个数.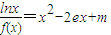 的根的个数.
的根的个数.