题目内容
已知函数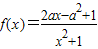 (x∈R),其中a∈R.
(x∈R),其中a∈R.(I)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(II)当a≠0时,求函数f(x)的单调区间与极值.
【答案】分析:(I)把a=1代入,先对函数求导,然后求f(2),根据导数的几何意义可知,该点切线的斜率k=f′(2),从而求出切线方程.
(II)先对函数求导,分别解f′(x)>0,f′(x)<0,解得函数的单调区间,根据函数的单调性求函数的极值.
解答:解:
(I)解:当a=1时, .
.
又 .
.
所以,曲线y=f(x)在点(2,f(2))处的切线方程为 ,即6x+25y-32=0.
,即6x+25y-32=0.
(II)解: =
= .
.
由于a≠0,以下分两种情况讨论.
(1)当a>0时,令f'(x)=0,得到 .当x变化时,f'(x),f(x)的变化情况如下表:
.当x变化时,f'(x),f(x)的变化情况如下表:

所以f(x)在区间 ,(a,+∞)内为减函数,在区间
,(a,+∞)内为减函数,在区间 内为增函数.
内为增函数.
函数f(x)在 处取得极小值
处取得极小值 ,且
,且 .
.
函数f(x)在x2=a处取得极大值f(a),且f(a)=1.
(2)当a<0时,令f'(x)=0,得到 .当x变化时,f'(x),f(x)的变化情况如下表:
.当x变化时,f'(x),f(x)的变化情况如下表:

所以f(x)在区间(-∞,a) 内为增函数,在区间
内为增函数,在区间 内为减函数.
内为减函数.
函数f(x)在x1=a处取得极大值f(a),且f(a)=1.
函数f(x)在 处取得极小值
处取得极小值 ,且
,且 .
.
点评:本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.
(II)先对函数求导,分别解f′(x)>0,f′(x)<0,解得函数的单调区间,根据函数的单调性求函数的极值.
解答:解:
(I)解:当a=1时,
 .
.又
 .
.所以,曲线y=f(x)在点(2,f(2))处的切线方程为
 ,即6x+25y-32=0.
,即6x+25y-32=0.(II)解:
 =
= .
.由于a≠0,以下分两种情况讨论.
(1)当a>0时,令f'(x)=0,得到
 .当x变化时,f'(x),f(x)的变化情况如下表:
.当x变化时,f'(x),f(x)的变化情况如下表:
所以f(x)在区间
 ,(a,+∞)内为减函数,在区间
,(a,+∞)内为减函数,在区间 内为增函数.
内为增函数.函数f(x)在
 处取得极小值
处取得极小值 ,且
,且 .
.函数f(x)在x2=a处取得极大值f(a),且f(a)=1.
(2)当a<0时,令f'(x)=0,得到
 .当x变化时,f'(x),f(x)的变化情况如下表:
.当x变化时,f'(x),f(x)的变化情况如下表:
所以f(x)在区间(-∞,a)
 内为增函数,在区间
内为增函数,在区间 内为减函数.
内为减函数.函数f(x)在x1=a处取得极大值f(a),且f(a)=1.
函数f(x)在
 处取得极小值
处取得极小值 ,且
,且 .
.点评:本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.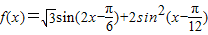 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.