题目内容
8.a,b是任意实数,a>b,且a≠0,则下列结论正确的是( )| A. | 3-a<3-b | B. | $\frac{b}{a}$<1 | C. | lg(a-b)>lg$\frac{1}{a-b}$ | D. | a2>b2 |
分析 根据指数函数的图象和性质,对数函数的图象和性质,不等式的基本性质逐一分析给定四个答案的真假,可得答案.
解答 解:∵a>b,且a≠0,
∴-a<-b,
∴3-a<3-b,故A正确;
当0>a>b时,$\frac{b}{a}$>1,故B错误;
当a-b∈(0,1]时,$\frac{1}{a-b}$∈[1,+∞),
lg(a-b)≤lg$\frac{1}{a-b}$,故C错误;
当a=1,b=-1时,a>b,且a≠0,
但a2=b2,故D错误;
故选:A
点评 本题以命题的真假判断与应用为载体,考查了指数函数的图象和性质,对数函数的图象和性质,不等式的基本性质等知识点,难度中档.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
16.
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.
| 商品名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.

20.复数z1,z2在复平面内对应的点的坐标分别为(0,2),(1,-1),则$\frac{z_1}{z_2}$的模为( )
| A. | 1 | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
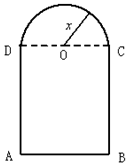 如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径
如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径