题目内容
已知函数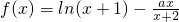 ,它在原点处的切线恰为x轴.
,它在原点处的切线恰为x轴.
(1)求f(x)的解析式;
(2)证明:当x>0时,f(x)>0;
(3)证明: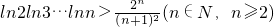 .
.
解:(1)由题意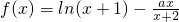 得,
得,
f′(x)= -
-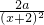 ,
,
由于函数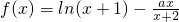 在原点处的切线恰为x轴.
在原点处的切线恰为x轴.
∴f′(0)=0,即1-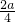 =0,
=0,
∴a=2.
∴f(x)的解析式f(x)=ln(1+x)- ,
,
(2)当x≥0时,f′(x)=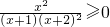 ,
,
∴f(x)在[0,+∞)上是增函数,且f(0)=0,
∴当x>0时,f(x)>f(0)=0,
即当x>0时,f(x)>0.
(3)由(2)知,当x>0时,ln(1+x)> ,
,
∴ln2> ,ln3>
,ln3>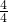 ,ln4>
,ln4> ,…,lnn>
,…,lnn>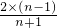 ,(n≥2),
,(n≥2),
以上各式相乘,得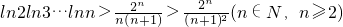 ,
,
从而结论成立.
分析:(1)先根据题意求出函数的导数f′(x),再利用导数的几何意义得f′(0)=0,从而求出a值,最后写出f(x)的解析式;
(2)当x≥0时,f′(x)=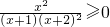 ,利用导数与单调性的关系得f(x)在[0,+∞)上是增函数,且f(0)=0,即可证得结论;
,利用导数与单调性的关系得f(x)在[0,+∞)上是增函数,且f(0)=0,即可证得结论;
(3)由(2)知,当x>0时,ln(1+x)> ,分别令x=1,2,3,…,n.得到n个不等关系,再将以上各式相乘即得.
,分别令x=1,2,3,…,n.得到n个不等关系,再将以上各式相乘即得.
点评:本小题主要考查导数的几何意义、函数单调性的应用、不等式的证明等基础知识,考查运算求解能力、化归与转化思想.属于中档题.
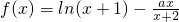 得,
得,f′(x)=
 -
-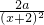 ,
,由于函数
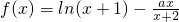 在原点处的切线恰为x轴.
在原点处的切线恰为x轴.∴f′(0)=0,即1-
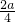 =0,
=0,∴a=2.
∴f(x)的解析式f(x)=ln(1+x)-
 ,
,(2)当x≥0时,f′(x)=
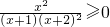 ,
,∴f(x)在[0,+∞)上是增函数,且f(0)=0,
∴当x>0时,f(x)>f(0)=0,
即当x>0时,f(x)>0.
(3)由(2)知,当x>0时,ln(1+x)>
 ,
,∴ln2>
 ,ln3>
,ln3>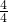 ,ln4>
,ln4> ,…,lnn>
,…,lnn>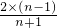 ,(n≥2),
,(n≥2),以上各式相乘,得
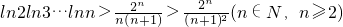 ,
,从而结论成立.
分析:(1)先根据题意求出函数的导数f′(x),再利用导数的几何意义得f′(0)=0,从而求出a值,最后写出f(x)的解析式;
(2)当x≥0时,f′(x)=
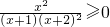 ,利用导数与单调性的关系得f(x)在[0,+∞)上是增函数,且f(0)=0,即可证得结论;
,利用导数与单调性的关系得f(x)在[0,+∞)上是增函数,且f(0)=0,即可证得结论;(3)由(2)知,当x>0时,ln(1+x)>
 ,分别令x=1,2,3,…,n.得到n个不等关系,再将以上各式相乘即得.
,分别令x=1,2,3,…,n.得到n个不等关系,再将以上各式相乘即得.点评:本小题主要考查导数的几何意义、函数单调性的应用、不等式的证明等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

练习册系列答案
相关题目
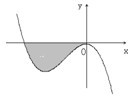
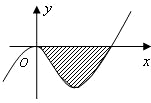 已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为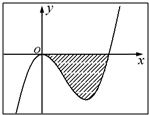 已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为
已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为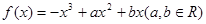 的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为
的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为 ,则a的值为
,则a的值为