题目内容
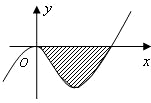已知函数f（x）=x3+ax2+bx（a，b∈R）的图象如图所示，它与直线y=0在原点处相切，此切线与函数图象所围区域（图中阴影部分）的面积为| 27 | 4 |
分析：由图可知f（x）=0得到x的解确定出b的值，确定出f（x）的解析式，由于阴影部分面积为
，利用定积分求面积的方法列出关于a的方程求出a并判断a的取舍即可．
| 27 |
| 4 |
解答：解：由图知方程f（x）=0有两个相等的实根x1=x2=0，于是b=0，
∴f（x）=x2（x+a），有
=
[0-(x3+ax2)]dx=-(
+
)
=
，
∴a=±3．
又-a＞0?a＜0，得a=-3．
故答案为：-3．
∴f（x）=x2（x+a），有
| 27 |
| 4 |
| ∫ | -a 0 |
| x4 |
| 4 |
| ax3 |
| 3 |
|
| a4 |
| 12 |
∴a=±3．
又-a＞0?a＜0，得a=-3．
故答案为：-3．
点评：考查学生利用定积分的方法求平面图形面积的能力．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|