题目内容
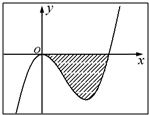已知函数f（x）=x3+ax2+bx（a，b∈R）的图象如图所示，它与直线y=0在原点处相切，此切线与函数图象所围区域（图中阴影部分）的面积为| 4 | 3 |
-2
-2
．分析：由题意可得f′（0）=b=0，代入可得解析式为f（x）=x3+ax2，令其为0可解得图中的交点坐标，进而可得S=
(-x3-ax2)dx=
，解之可得答案．
| ∫ | -a 0 |
| 4 |
| 3 |
解答：解：由题意可知f′（x）=3x2+2ax+b，
因为图象与直线y=0在原点处相切，∴f′（0）=b=0，
故f（x）=x3+ax2=x2（x+a），令其为0可解得x=0或x=-a，
故图中的与x轴交点处（原点右侧）的横坐标为-a，（a＜0）
故S=
(-x3-ax2)dx=（-
x4-
x3）
=-
a4+
a3=
a4=
，解得a=-2，或a=2（舍去）
故答案为：-2
因为图象与直线y=0在原点处相切，∴f′（0）=b=0，
故f（x）=x3+ax2=x2（x+a），令其为0可解得x=0或x=-a，
故图中的与x轴交点处（原点右侧）的横坐标为-a，（a＜0）
故S=
| ∫ | -a 0 |
| 1 |
| 4 |
| a |
| 3 |
| | | -a 0 |
=-
| 1 |
| 4 |
| a |
| 3 |
| 1 |
| 12 |
| 4 |
| 3 |
故答案为：-2
点评：本题考查定积分的求解，涉及函数的切线问题，属基础题．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|