题目内容
已知函数f(x)=alnx,g(x)=-x2+(a+2)x+1.
(1)若直线y=2x与曲线y=f(x)相切,求实数a的值;
(2)若f(x)≥g(x)对一切实数x∈[1,e]恒成立,求实数a的取值范围.
(1)若直线y=2x与曲线y=f(x)相切,求实数a的值;
(2)若f(x)≥g(x)对一切实数x∈[1,e]恒成立,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(1)先求出切点坐标,再代入f(x)=alnx,即可求实数a的值;
(2)f(x)≥g(x),即alnx≥-x2+(a+2)x+1.也即a(x-lnx)≤x2-2x-1,此式对一切实数x∈[1,e]恒成立.进一步转化为a ≤
,此式对一切实数x∈[1,e]恒成立,求最值即可.
(2)f(x)≥g(x),即alnx≥-x2+(a+2)x+1.也即a(x-lnx)≤x2-2x-1,此式对一切实数x∈[1,e]恒成立.进一步转化为a ≤
| x2-2x-1 |
| x-lnx |
解答:
解:(1)设切点为(x0,y0),
∵f(x)=alnx,∴f′(x)=
,
∴切线方程为y-alnx0=
(x-x0). …2分
∵切线y=2x过原点,∴-alnx0=-a.
则x0=e,y0=2e.即切点为(e,2e). …4分
代入y=f(x),得a=2e. …6分
(2)f(x)≥g(x),即alnx≥-x2+(a+2)x+1.
也即a(x-lnx)≤x2-2x-1,此式对一切实数x∈[1,e]恒成立.
设h(x)=x-lnx,∵h′(x)=1-
=
>0在x∈[1,e]恒成立.
∴h(x)=x-lnx在[1,e]上是增函数,h(x)≥h(1)=1. …8分
∴a ≤
,此式对一切实数x∈[1,e]恒成立. …10分
设u(x)=
,
则u′(x)=
=
. …13分
当x∈(1,e)时,-2xlnx+2x=2x(1-lnx)>0.则u'(x)>0.
而u(x)在[1,e]是图象不间断,∴u(x)的最小值为u(1)=-2.
∴a≤-2. …16分.
∵f(x)=alnx,∴f′(x)=
| a |
| x |
∴切线方程为y-alnx0=
| a |
| x0 |
∵切线y=2x过原点,∴-alnx0=-a.
则x0=e,y0=2e.即切点为(e,2e). …4分
代入y=f(x),得a=2e. …6分
(2)f(x)≥g(x),即alnx≥-x2+(a+2)x+1.
也即a(x-lnx)≤x2-2x-1,此式对一切实数x∈[1,e]恒成立.
设h(x)=x-lnx,∵h′(x)=1-
| 1 |
| x |
| x-1 |
| x |
∴h(x)=x-lnx在[1,e]上是增函数,h(x)≥h(1)=1. …8分
∴a ≤
| x2-2x-1 |
| x-lnx |
设u(x)=
| x2-2x-1 |
| x-lnx |
则u′(x)=
(2x-2)(x-lnx)-(x2-2x-1)(1-
| ||
| (x-lnx)2 |
| (x-1)(x2-2xlnx+2x+1) |
| x(x-lnx)2 |
当x∈(1,e)时,-2xlnx+2x=2x(1-lnx)>0.则u'(x)>0.
而u(x)在[1,e]是图象不间断,∴u(x)的最小值为u(1)=-2.
∴a≤-2. …16分.
点评:本题考查导数在最大值、最小值问题中的应用,考查利用导数研究曲线上某点切线方程,正确分离参数求最值是关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
下面四个条件中,使a>b成立的充分不必要条件是( )
| A、a3>b3 |
| B、a>b+1 |
| C、a2>b2 |
| D、a>b-1 |
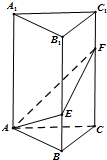 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=