题目内容
已知:在数列{an}中,a1= ,an+1=
,an+1= an+
an+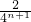 .
.
(1)令bn=4nan,求证:数列{bn}是等差数列;
(2)若Sn为数列{an}的前n项的和,Sn+λnan≥ 对任意n∈N*恒成立,求实数λ的最小值.
对任意n∈N*恒成立,求实数λ的最小值.
解:(1)由an+1= an+
an+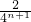 ,
,
得4n+1an+1=4nan+2.
所以bn+1=bn+2,即bn+1-bn=2.
故数列{bn}是首项为1,公差为2的等差数列.
(2)因为数列{bn}是首项为1,公差为2的等差数列,
所以bn=1+2(n-1)=2n-1.
因为bn=4nan,
所以an= .
.
则Sn= +
+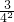 +
+ +…+
+…+ +
+ .
.
又 Sn=
Sn= +
+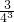 +
+ +…+
+…+ +
+ .
.
所以 Sn=
Sn= +2(
+2( +
+ +
+ +…+
+…+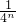 )-
)-
= +2×
+2× -
- .
.
所以Sn= -
- ×
×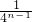 -
- ×
×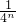 .
.
因为Sn+λnan≥ 对任意n∈N*恒成立,
对任意n∈N*恒成立,
所以 -
- ×
×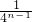 -
- ×
×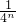 +λ×
+λ× ≥
≥ 对任意n∈N*恒成立.
对任意n∈N*恒成立.
即λ≥ ×
× +
+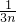 对任意n∈N*恒成立
对任意n∈N*恒成立
因为n≥1,2n-1≥1,
所以 ×
× ≤
≤ ,当且仅当n=1时取等号.
,当且仅当n=1时取等号.
又因为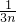 ≤
≤ ,当且仅当n=1时取等号.
,当且仅当n=1时取等号.
所以 ×
× +
+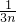 ≤
≤ ,当且仅当n=1时取等号
,当且仅当n=1时取等号
所以λ≥ ,所以λ的最小值为
,所以λ的最小值为 .
.
分析:(1)由题设条件知4n+1an+1=4nan+2.所以bn+1=bn+2,所以数列{bn}是首项为1,公差为2的等差数列.
(2)由题设条件知bn=1+2(n-1)=2n-1.再由bn=4nan,知an= .再由错位相减法可求出Sn=
.再由错位相减法可求出Sn= -
- ×
×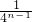 -
- ×
×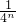 .然后根据Sn+λnan≥
.然后根据Sn+λnan≥ 对任意n∈N*恒成立,可求出实数λ的最小值.
对任意n∈N*恒成立,可求出实数λ的最小值.
点评:本题考查数列的性质和应用,解题时要注意错位相减法的灵活运用,认真审题,仔细解答.
 an+
an+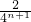 ,
,得4n+1an+1=4nan+2.
所以bn+1=bn+2,即bn+1-bn=2.
故数列{bn}是首项为1,公差为2的等差数列.
(2)因为数列{bn}是首项为1,公差为2的等差数列,
所以bn=1+2(n-1)=2n-1.
因为bn=4nan,
所以an=
 .
.则Sn=
 +
+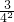 +
+ +…+
+…+ +
+ .
.又
 Sn=
Sn= +
+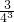 +
+ +…+
+…+ +
+ .
.所以
 Sn=
Sn= +2(
+2( +
+ +
+ +…+
+…+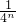 )-
)-
=
 +2×
+2× -
- .
.所以Sn=
 -
- ×
×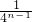 -
- ×
×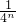 .
.因为Sn+λnan≥
 对任意n∈N*恒成立,
对任意n∈N*恒成立,所以
 -
- ×
×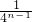 -
- ×
×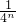 +λ×
+λ× ≥
≥ 对任意n∈N*恒成立.
对任意n∈N*恒成立.即λ≥
 ×
× +
+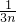 对任意n∈N*恒成立
对任意n∈N*恒成立因为n≥1,2n-1≥1,
所以
 ×
× ≤
≤ ,当且仅当n=1时取等号.
,当且仅当n=1时取等号.又因为
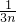 ≤
≤ ,当且仅当n=1时取等号.
,当且仅当n=1时取等号.所以
 ×
× +
+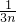 ≤
≤ ,当且仅当n=1时取等号
,当且仅当n=1时取等号所以λ≥
 ,所以λ的最小值为
,所以λ的最小值为 .
.分析:(1)由题设条件知4n+1an+1=4nan+2.所以bn+1=bn+2,所以数列{bn}是首项为1,公差为2的等差数列.
(2)由题设条件知bn=1+2(n-1)=2n-1.再由bn=4nan,知an=
 .再由错位相减法可求出Sn=
.再由错位相减法可求出Sn= -
- ×
×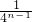 -
- ×
×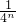 .然后根据Sn+λnan≥
.然后根据Sn+λnan≥ 对任意n∈N*恒成立,可求出实数λ的最小值.
对任意n∈N*恒成立,可求出实数λ的最小值.点评:本题考查数列的性质和应用,解题时要注意错位相减法的灵活运用,认真审题,仔细解答.

练习册系列答案
相关题目