题目内容
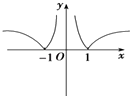
【题目】已知函数
有两个零点
， 
，则下面说法正确的是（ ）
A. 
B. 
C. 
D. 有极小值点
，且
【答案】D
【解析】由题意得,因为
，所以
,设
则由图像法知
, 
, 
,解得
因此
,
令
,则
,
所以
因此
,因此A错误；
方程
有两个不等的根,即
与
有两个不同的交点.
因为
所以
在
上单调递减,且
，在
上单调递减且
，在
上单调递增且
，且
， 
B错误;
令
,则
所以
因此
,因此C错误;
由
, 
当
时
当
时
所以
有极小值点
由
得
因此
所以
所以
,D正确. 选D.
点晴：本题考查的是利用导数解决函数的极值点偏移问题.解决这类问题有三个关键步骤:第一步求导数，根据导函数的正负确定函数的单调增，减区间和极值点，第二步在相对小区间上构造函数和0比较大小 ，第三步在相对大区间上利用已知函数的单调性得到目标式的大小比较.
练习册系列答案
相关题目
【题目】在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.
（1）根据以上数据建立一个
列联表；
（2）判断性别与休闲方式是否有关系.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
【题目】高考复习经过二轮“见多识广”之后，为了研究考前“限时抢分”强化训练次数
与答题正确率
﹪的关系，对某校高三某班学生进行了关注统计，得到如下数据：
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
（1）求
关于
的线性回归方程，并预测答题正确率是100﹪的强化训练次数；
（2）若用
表示统计数据的“强化均值”（精确到整数），若“强化均值”的标准差在区间
内，则强化训练有效，请问这个班的强化训练是否有效？
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
＝
， 
＝
－
，
样本数据
的标准差为： 
