题目内容
7. 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )| A. | 0 | B. | 3$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | -$\sqrt{2}$ |
分析 由已知中的函数的图象,我们易求出函数的解析式,进而分析出函数的性质,根据函数是一个周期函数,我们可以将f(1)+f(2)+…+f(2006)转化为一个数列求和问题,然后利用分组求和法,即可得到答案.
解答 解:由函数图象可得:A=2,T=2(6-2)=8=$\frac{2π}{ω}$,故解得:ω=$\frac{π}{4}$,可得函数解析式为:f(x)=2sin$\frac{π}{4}$x,
所以,有:f(1)=$\sqrt{2}$
f(2)=2
f(3)=$\sqrt{2}$
f(4)=0
f(5)=-$\sqrt{2}$
f(6)=-2
f(7)=-$\sqrt{2}$
f(8)=0
f(9)=$\sqrt{2}$
…
观察规律可知函数f(x)的值以8为周期,且f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)+f(8)=0,
由于2015=251*8+7,故可得:f(1)+f(2)+f(3)+…+f(2015)=f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)=0.
故选:A.
点评 本题考查的知识点是由y=Asin(ωx+φ)的部分图象确定其解析式及数列求和,其中根据函数的图象,求出函数的解析式,进而分析出函数的性质是解答本题的关键.

练习册系列答案
相关题目
15.实数x,y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{x+2y-3≥0}\\{2x+y-3≤0}\end{array}\right.$,则下列点中不能使u=2x+y取得最大值的是( )
| A. | (1,1) | B. | (0,3) | C. | ($\frac{1}{2}$,2) | D. | ($\frac{3}{2}$,0) |
19.设复数z1=1+i,z2=x+2i(x∈R),若z1z2为纯虚数,则x=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
16.集合M={x|lgx>0},N={x|x2≤4},则M∩N=( )
| A. | (0,2] | B. | (0,2) | C. | (1,2] | D. | (1,2) |
 中,
中, 且
且 ,则
,则 ( )
( ) B.3
B.3  D.7
D.7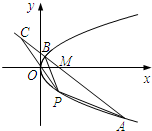 如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.
如图,在平面直角坐标系xOy中,点A(8,-4),P(2,t)(t<0)在抛物线y2=2px(p>0)上.