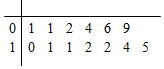
题目内容
20．已知集合A={x|x2-1≥0，x∈R}，B={x|0≤x＜3，x∈R}，则A∩B=（ ）| A． | {x|1＜x＜3，x∈R} | B． | {x|1≤x≤3，x∈R} | C． | {x|1≤x＜3，x∈R} | D． | {x|0＜x＜3，x∈R} |
分析 求出A中不等式的解集确定出A，找出A与B的交集即可．
解答 解：由A中不等式变形得：（x+1）（x-1）≥0，
解得：x≤-1或x≥1，即A={x|x≤-1或x≥1，x∈R}，
∵B={x|0≤x＜3，x∈R}，
∴A∩B={x|1≤x＜3，x∈R}，
故选：C．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．已知集合A={0，1，2}，B={x|x2=1}，则A∩B等于（ ）
| A． | {-1，1} | B． | {0，1} | C． | {1} | D． | {-1，0，1} |
11．如果实数x，y满足条件$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-y+2≥0}\\{x-a≤0}\end{array}\right.$，若z=$\frac{y-1}{x+1}$的最小值小于$\frac{1}{2}$，则实数a的取值范围是（ ）
| A． | （-∞，1） | B． | （1，+∞） | C． | （$\frac{1}{5}$，1） | D． | （$\frac{1}{5}$，+∞） |
8．若非空集合A={x|a+1≤x≤3a-5}，集合B={x|1≤x≤16}，则满足A⊆（A∩B）的实数a的取值范围是（ ）
| A． | [0，7] | B． | [7，15] | C． | [3，7] | D． | [3，15] |
15．若实数x，y满足$\left\{\begin{array}{l}x-y-2≥0\\ 2x+y-2≤0\\ y+4≥0.\end{array}\right.$，则目标函数z=4x+3y的最大值为（ ）
| A． | 0 | B． | $\frac{10}{3}$ | C． | 12 | D． | 20 |
某地区交管部门为了对该地区驾驶员的某项考试成绩进行分析，随机抽取了15分到45分之间的1000名学员的成绩，并根据这1000名驾驶员的成绩画出样本的频率分布直方图（如图），则成绩在[30，35）内的驾驶员人数共有300．