题目内容
已知Sn=4-an-
,求an与Sn.
| 1 |
| 2n-2 |
考点:数列递推式
专题:等差数列与等比数列
分析:由数列递推式求出首项,取n=n-1得另一递推式,作差后可得数列{2nan}构成以2为首项,以2为公差的等差数列,由等差数列的通项公式求得an,然后利用错位相减法求出其前n项和Sn.
解答:
解:由Sn=4-an-
,得a1=S1=4-a1-
,解得:a1=1;
当n≥2时,Sn-1=4-an-1-
,
两式作差得:an=-an+an-1-
+
,
即an=
an-1+
.
∴2nan-2n-1an-1=2(n≥2),
∴数列{2nan}构成以2为首项,以2为公差的等差数列,
则2nan=2+2(n-1)=2n,
∴an=
;
Sn=
+
+
+…+
,
Sn=
+
+…+
+
,
两式作差得:
Sn=1+
+
+…+
-
=
-
=2(1-
)-
,
∴Sn=4(1-
)-
.
| 1 |
| 2n-2 |
| 1 |
| 2-1 |
当n≥2时,Sn-1=4-an-1-
| 1 |
| 2n-3 |
两式作差得:an=-an+an-1-
| 1 |
| 2n-2 |
| 1 |
| 2n-3 |
即an=
| 1 |
| 2 |
| 1 |
| 2n-1 |
∴2nan-2n-1an-1=2(n≥2),
∴数列{2nan}构成以2为首项,以2为公差的等差数列,
则2nan=2+2(n-1)=2n,
∴an=
| n |
| 2n-1 |
Sn=
| 1 |
| 20 |
| 2 |
| 21 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| n-1 |
| 2n-1 |
| n |
| 2n |
两式作差得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
1×(1-
| ||
1-
|
| n |
| 2n |
| 1 |
| 2n |
| n |
| 2n |
∴Sn=4(1-
| 1 |
| 2n |
| n |
| 2n-1 |
点评:本题考查了数列递推式,考查了等差关系的确定,训练了错位相减法求数列的和,是中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
已知A(2,-4),B(0,6),C(-8,10),则
+2
为( )
| AB |
| BC |
| A、(18,18) |
| B、(-18,18) |
| C、(18,-18) |
| D、(-18,-18) |

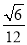 B.
B.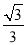 C.
C.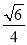 D.
D.
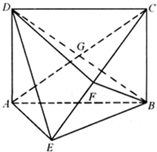 如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.
如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.