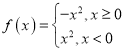题目内容
【题目】已知![]() (a>0)是定义在R上的偶函数,
(a>0)是定义在R上的偶函数,
(1)求实数a的值;
(2)判断并证明函数![]() 在
在![]() 的单调性;
的单调性;
(3)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)函数
;(2)函数![]() 在
在![]() 上是单调递增的;(3)
上是单调递增的;(3)![]() .
.
【解析】
试题(1)由函数![]() 为偶函数,得
为偶函数,得![]() ,代入函数表达式,化简求得
,代入函数表达式,化简求得![]() ,由
,由![]() ,得
,得![]() ;(2)用定义证明函数在
;(2)用定义证明函数在![]() 上单调递增的步骤:设值—作差、变形—判断符号—得出结论;(3)将不等式
上单调递增的步骤:设值—作差、变形—判断符号—得出结论;(3)将不等式![]() 转化为
转化为![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,只需求得函数的最小值,代入不等式即可求得m的范围.
,只需求得函数的最小值,代入不等式即可求得m的范围.
试题解析:解析:(1)因为f(x)为偶函数,所以f(-x)=f(x)
即![]() =
=![]()
∴![]() ex-
ex-![]() e-x=0,
e-x=0,
∴![]() (ex-e-x)=0,
(ex-e-x)=0,
∴a-![]() =0,即a=±1.
=0,即a=±1.
而a>0,∴![]() ,∴f(x)=ex+e-x.
,∴f(x)=ex+e-x.
(2)函数![]() 在
在![]() 上是单调递增的.
上是单调递增的.
证明:任取![]() 且x1<x2,
且x1<x2,

∴f(x)在![]() 上是增函数.
上是增函数.
(3)由题意,![]() 在
在![]() 上恒成立,
上恒成立,
则只需![]()
∵f(x)为偶函数,且f(x)在![]() 上是增函数∴f(x)在(-∞,0)上是减函数,
上是增函数∴f(x)在(-∞,0)上是减函数,
∴f(x)的最小值为![]()
则有![]() ,因此
,因此![]() .
.

练习册系列答案
相关题目
【题目】某工厂生产一种产品,根据预测可知,该产品的产量平稳增长,记2015年为第1年,第x年与年产量![]() (万件)之间的关系如下表所示:
(万件)之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
| 4.00 | 5.52 | 7.00 | 8.49 |
现有三种函数模型:![]() ,
,![]() ,
,![]()
(1)找出你认为最适合的函数模型,并说明理由,然后选取![]() 这两年的数据求出相应的函数解析式;
这两年的数据求出相应的函数解析式;
(2)因受市场环境的影响,2020年的年产量估计要比预计减少30%,试根据所建立的函数模型,估计2020年的年产量.