题目内容
7.设奇函数f(x)在(0,+∞)上为减函数,且f(2)=0,则不等式$\frac{f(x)+2f(-x)}{x}$<0的解集为( )| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
分析 根据函数奇偶性和单调性之间的关系即可得到结论.
解答  解:∵奇函数f(x)在(0,+∞)上为减函数,且f(2)=0,
解:∵奇函数f(x)在(0,+∞)上为减函数,且f(2)=0,
∴函数f(x)在(-∞,0)上为减函数,且f(-2)=f(2)=0,
作出函数f(x)的草图如图:
∵f(x)是奇函数,∴不等式等价为$\frac{f(x)-2f(x)}{x}=\frac{-f(x)}{x}<0$,即$\frac{f(x)}{x}$>0,
即$\left\{\begin{array}{l}{x>0}\\{f(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)<0}\end{array}\right.$,
则0<x<2或-2<x<0,
故不等式$\frac{{f(x)-f({-x})}}{x}$>0的解集是(-2,0)∪(0,2),
故选:C.
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
15.已知一个正四面体纸盒的棱长为$2\sqrt{6}$,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A. | 1 | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
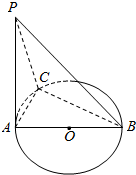 AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.
AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.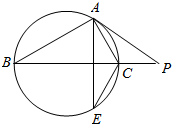 若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( )
若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( )