题目内容
用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3，(n∈N*) 能被9整除”，要利用归纳假设证n＝k＋1(k∈N*)时的情况，只需展开( )
A．(k＋3)3 B．(k＋2)3
C．(k＋1)3 D．(k＋1)3＋(k＋2)3
解析：假设n＝k(k∈N*)时，k3＋(k＋1)3＋(k＋2)3能被9整除，当n＝k＋1时，(k＋1
)3＋(k＋2)3＋(k＋3)3为了能用上面的归纳假设证明，只需将(k＋3)3展开，让其出现k3即可．故应选A.
答案：
A
练习册系列答案
相关题目
(n∈N+)时，从“n=k到n=k+
B.
D.
+
+
+…+
≥
(n∈N*)”时，由“n=k到n=k+1”，不等式左边应添加的项是( )
+
+
-
+
-
-
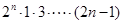(n∈N*)时，从n＝k到n＝k＋1，左端需要增加的代数式为（ ）
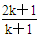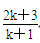
D．
D．. 