题目内容
用数学归纳法证明n(n+1)(2n+1)能被6整除时,由归纳假设推证n=k+1时命题成立,需将n=k+1时的原式表示成( )
分析:在使用数学归纳法证明“n(n+1)(2n+1)能被6整除”的过程中,由n=k时成立,即“k(k+1)(2k+1)能被6整除”时,为了使用已知结论对(k+1)(k+2)(2k+3)进行论证,在分解的过程中一定要分析出含k(k+1)(2k+1)+6(k+1)2的情况.
解答:解:假设n=k时命题成立.
即:k(k+1)(2k+1)能被6整除.
当n=k+1时,(k+1)(k+2)(2k+3)
=(k+1)(k+2)(2k+1+2)
=(k+1)(k+2)(2k+1)+2(k+1)(k+2)
=k(k+1)(2k+1)+2(k+1)(2k+1)+2(k+1)(k+2)
=k(k+1)(2k+1)+6(k+1)2.
故选:C.
即:k(k+1)(2k+1)能被6整除.
当n=k+1时,(k+1)(k+2)(2k+3)
=(k+1)(k+2)(2k+1+2)
=(k+1)(k+2)(2k+1)+2(k+1)(k+2)
=k(k+1)(2k+1)+2(k+1)(2k+1)+2(k+1)(k+2)
=k(k+1)(2k+1)+6(k+1)2.
故选:C.
点评:本题考查数学归纳法,数学归纳法是证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
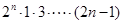 (n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
(n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )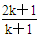 D.
D.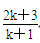
 D..
D..