Question

用数学归纳法证明(n＋1)(n＋2)(n＋3)…(n＋n)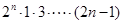＝ (n∈N^*)时，从n＝k到n＝k＋1，左端需要增加的代数式为（   ）

A．2k＋1            B．2(2k＋1)          C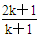．           D．

 

Answer 1

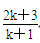
【答案】

B

【解析】

试题分析：从n＝k到n＝k＋1，右边从变为，增加的代数式是2(2k＋1)。故选B。

考点：数学归纳法

点评：本题用到的数学归纳法，在高中数学中常用来证明等式成立和数列通项公式成立。若要证明一个与自然数n有关的命题P(n），有如下步骤：

（1）证明当n取第一个值时命题成立。对于一般数列取值为0或1，但也有特殊情况；

（2）假设当n=k（k≥，k为自然数）时命题成立，证明当n=k+1时命题也成立。

综合（1）（2），对一切自然数n（≥），命题P(n）都成立。