题目内容
3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数:
(1)选其中5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体站成一排,男、女各站在一起;
(4)全体站成一排,男生不能站在一起;
(5)全体站成一排,甲不站排头也不站排尾.
解 (1)问题即为从7个不同元素中选出5个全排列,有A =2 520(种)排法.
=2 520(种)排法.
(2)前排3人,后排4人,相当于排成一排,共有A =5 040(种)排法.
=5 040(种)排法.
(3)相邻问题(捆绑法):男生必须站在一起,是男生的全排列,有A 种排法;女生必须站在一起,是女生的全排列,有A
种排法;女生必须站在一起,是女生的全排列,有A 种排法;全体男生、女生各视为一个元素,有A
种排法;全体男生、女生各视为一个元素,有A 种排法,由分步乘法计数原理知,共有A
种排法,由分步乘法计数原理知,共有A ·A
·A ·A
·A =288(种).
=288(种).
(4)不相邻问题(插空法):先安排女生共有A 种排法,男生在4个女生隔成的五个空中安排共有A
种排法,男生在4个女生隔成的五个空中安排共有A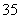 种排法,故A
种排法,故A ·A
·A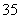 =1 440(种).
=1 440(种).
(5)先安排甲,从除去排头和排尾的5个位中安排甲,有A =5种排法;再安排其他人,有A
=5种排法;再安排其他人,有A =720(种)排法.所以共有A
=720(种)排法.所以共有A ·A
·A =3 600(种)排法.
=3 600(种)排法.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
高三某班学生每周用于物理学习的时间x(单位:小时)与物理成绩y(单位:分)之间有如下关系:
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
根据上表可得回归方程的斜率为3.53,则回归直线在y轴上的截距为________.(答案保留到0.1)
