题目内容
已知抛物线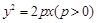 的焦点为
的焦点为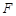 ,点
,点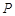 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,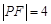 .
.
(1)求抛物线的方程;
(2) 设点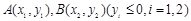 是抛物线上的两点,
是抛物线上的两点,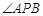 的角平分线与
的角平分线与 轴垂直,求
轴垂直,求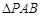 的面积最大时直线
的面积最大时直线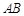 的方程.
的方程.
(1)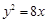 ;(2)
;(2)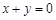
解析试题分析:(1)由于点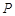 是抛物线上的一点,且其纵坐标为4,假设点
是抛物线上的一点,且其纵坐标为4,假设点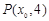 ,再通过
,再通过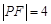 ,可得一个关于
,可得一个关于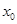 与
与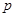 的关系式,在结合抛物线方程即可求出
的关系式,在结合抛物线方程即可求出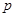 .从而求得抛物线的方程.
.从而求得抛物线的方程.
(2)因为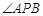 的角平分线与
的角平分线与 轴垂直,所以可知
轴垂直,所以可知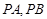 的倾斜角互补,即
的倾斜角互补,即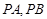 的斜率互为相反数.所以假设直线PA,联立抛物线方程即可得到点A的坐标,类比地求出点B的坐标.结合韦达定理,可以得到直线AB的斜率为定值-1.通过假设直线AB的方程,联立抛物线的方程,应用点到直线的距离,即可表示三角形的面积.再通过求最值即能到结论.
的斜率互为相反数.所以假设直线PA,联立抛物线方程即可得到点A的坐标,类比地求出点B的坐标.结合韦达定理,可以得到直线AB的斜率为定值-1.通过假设直线AB的方程,联立抛物线的方程,应用点到直线的距离,即可表示三角形的面积.再通过求最值即能到结论.
(1)设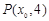 ,因为
,因为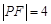 ,由抛物线的定义得
,由抛物线的定义得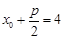 ,又
,又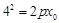 ,所以
,所以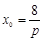 ,
,
因此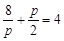 ,解得
,解得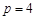 ,从而抛物线的方程为
,从而抛物线的方程为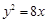 .
.
(2)由(1)知点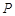 的坐标为
的坐标为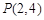 ,因为
,因为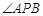 的角平分线与
的角平分线与 轴垂直,所以可知
轴垂直,所以可知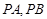 的倾斜角互补,即
的倾斜角互补,即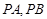 的斜率互为相反数
的斜率互为相反数
设直线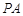 的斜率为
的斜率为 ,则
,则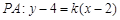 ,由题意
,由题意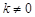 ,
,
把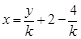 代入抛物线方程得
代入抛物线方程得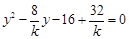 ,该方程的解为4、
,该方程的解为4、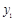 ,
,
由韦达定理得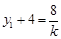 ,即
,即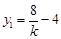 ,同理
,同理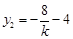 ,
,
所以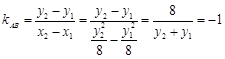 ,
,
设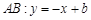 ,把
,把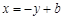 代入抛物线方程得
代入抛物线方程得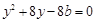 ,
,
由题意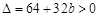 ,且
,且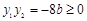 ,从而
,从而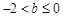
又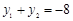 ,所以
,所以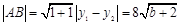 ,点
,点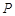 到
到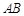 的距离
的距离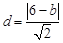 ,
,
因此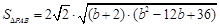 ,设
,设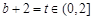 ,
,
则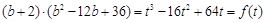 ,
,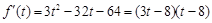
由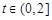 知
知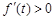 ,所以
,所以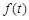 在
在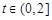 上为增函数,因此
上为增函数,因此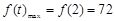 ,
,
即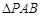 面积的最大值为
面积的最大值为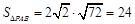 .
.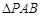 的面积取最大值时
的面积取最大值时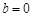 ,所以直线
,所以直线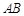 的方程为
的方程为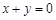 .
.
考点:1.抛物线的性质.2.函数的最值.3.等价变换.4.圆锥曲线与函数知识的交汇.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 :
: 左右焦点
左右焦点 、
、 的动直线
的动直线 相交于
相交于 点,与椭圆
点,与椭圆 分别交于
分别交于 不同四点,直线
不同四点,直线 的斜率
的斜率 、
、 、
、 、
、 满足
满足 .已知当
.已知当 轴重合时,
轴重合时, ,
, .
. 的方程;
的方程; ,使得
,使得 为定值.若存在,求出
为定值.若存在,求出 点坐标并求出此定值,若不存在,说明理由.
点坐标并求出此定值,若不存在,说明理由.
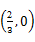 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.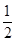 ,斜率为2的直线l过点A(2,3).
,斜率为2的直线l过点A(2,3).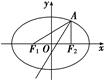
 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的长半轴长。
的长半轴长。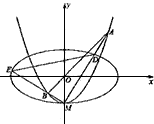
 的方程;
的方程; 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线 与
与 ;
; .问:是否存在直线
.问:是否存在直线 =
= ?请说明理由。
?请说明理由。 的离心率为
的离心率为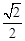 ,短轴端点分别为
,短轴端点分别为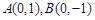 .
. ,
, 是椭圆
是椭圆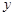 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与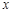 轴交于点
轴交于点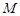 ,判断以线段
,判断以线段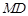 为直径的圆是否过点
为直径的圆是否过点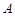 ,并说明理由.
,并说明理由.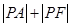 的最小值及此时P点的坐标.
的最小值及此时P点的坐标. 的两个焦点分别为
的两个焦点分别为 和
和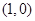 ,离心率
,离心率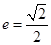 .
. (
(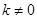 )与椭圆
)与椭圆 、
、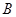 ,且线段
,且线段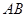
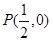 ,求实数
,求实数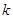 的取值范围.
的取值范围. 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
 、
、 表示出
表示出 垂直于
垂直于 轴;
轴; 的面积,证明
的面积,证明 、
、 ,再作与
,再作与 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.