题目内容
已知圆M：
，直线l：
，下面四个命题：
A.对任意实数k与q，直线l和圆M相切；
B.对任意实数k与q，直线l和圆M有公共点；
C.对任意实数q，必存在实数k，使得直线l与和圆M相切
D.对任意实数k，必存在实数q，使得直线l与和圆M相切
其中真命题的代号是______________（写出所有真命题的代号）
B,D
解析:
圆心坐标为（－cosq，sinq），
，说明对任意实数k与q，直线l与圆M相交或相切，故命题A、C不是真命题，命题B、D是真命题，答案选B、D. 另解：直线与圆均过原点，因此不论
为何值，直线与圆均有公共点。于是对任意的
与
，直线与圆相交或相切，故命题A不是真命题，命题B是真命题；当
时，圆M
与
轴相切，而不存在，故命题C不是真命题；而对任意实数k来说，必存在实数q，使得直线l与和圆M相切，故命题D是真命题。故选B、D.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
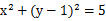，直线l：
．
，直线l：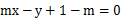
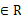（m∈R）． （Ⅰ）证明：不论m取什么实数，直线l与圆恒交于两点．
，直线L：
，直线L与圆C总有两个交点；
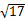，求直线L的倾斜角；
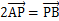,求此时直线L的方程.
，直线L：
，直线L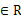与圆C总有两个交点；
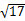，求直线L的倾斜角；
,求此时直线L的方程.